[Data Structure] Hash Table

in Computer Science on Data Structure


Hash Table 해시 테이블

  • 키(Key)에 데이터(Value)를 저장하는 데이터 구조
  • Key를 통해 바로 데이터를 받아올 수 있으므로, 속도가 획기적으로 빨라짐
  • 보통 배열로 미리 Hash Table 사이즈만큼 생성 후에 사용 (공간과 탐색 시간을 맞바꾸는 기법)
  • 캐쉬를 구현하는 등의 검색, 저장, 삭제, 읽기가 많이 필요한 경우 사용
  • 파이썬에서는 dictionary 타입으로 해시 테이블을 구현 가능

순차적으로 배열에 저장되어있는 자료를 삽입, 삭제, 탐색을 할 때는 일반적으로 시간복잡도가 O(n)이 되는데
해시 테이블로 자료를 저장한다면 일반적으로 삽입, 삭제, 탐색에 상수 시간 O(1) 밖에 걸리지 않음
(모든 경우에 충돌이 발생하는 최악의 경우 O(n)의 시간 복잡도가 듦)


장점

  • 데이터 저장/읽기 속도가 빠름 (검색 속도가 빠름)
  • 해시는 키에 대한 데이터가 있는지(중복) 확인이 쉬움

단점

  • 연결을 위한 별도 데이터 공간이 필요하므로 저장 공간 효율이 높지 않음
  • 데이터를 찾는 시간이 필요하므로 접근 속도가 느림
  • 중간 데이터 삭제 시, 앞뒤 데이터의 연결을 재구성해야 하는 부가적인 작업 필요
  • 순서와 상관없이 key만을 가지고 hash를 찾아 저장하기 때문에 상하관계가 있거나, 순서가 중요한 데이터의 경우 Hash Table은 어울리지 않음
    (파이썬 3.7 부터 표준 딕셔너리 dict 가 삽입 순서를 보존)


해시 관련 용어

  • 해시(Hash): 임의 값을 고정 길이로 변환하는 것
  • 해시 테이블(Hash Table): 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
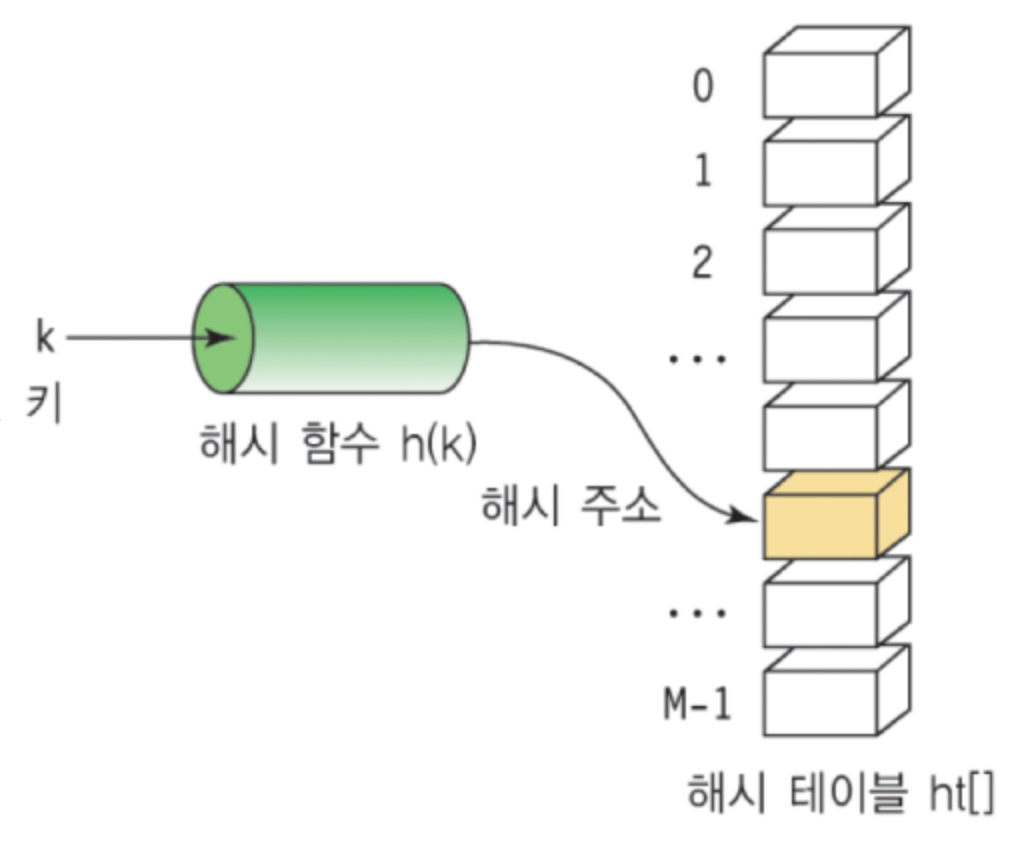
  • 해싱 함수(Hashing Function): Key에 대해 산술 연산을 이용해 데이터 위치를 찾을 수 있는 함수
  • 해시 값(Hash Value) 또는 해시 주소(Hash Address): Key를 해싱 함수로 연산해서, 해시 값을 알아내고, 이를 기반으로 해시 테이블에서 해당 Key에 대한 데이터 위치를 일관성있게 찾을 수 있음
  • 슬롯(Slot): 한 개의 데이터를 저장할 수 있는 공간


출처 : https://www.fun-coding.org/DS&AL1-6.html
일반적인 해시 테이블의 프로세스

충돌 (Hash collision)

충돌 해결 함수 (collision resolution method)를 통해서 충돌을 해결

해시 테이블을 구성함에 있어서 고려해야 할 사항

  1. table (list)
  2. Hash function
  3. Hash collision resolution method

해시 함수 (Hash function)

Division hash function
나머지 연산으로 key 값을 정하는 해시 함수

Perfect hash function
충돌이 일어나지 않고 1 to 1 으로 각각 다른 슬롯에 자료가 저장될 수 있게끔 하는 해시 함수
이상적인 해시 함수 (비현실적)

Universial hash function
두개의 서로 다른 키 값이 같은 슬롯에 저장 될 확률이 해시 테이블 사이즈에 반비례하는 함수

그 외에도
Multiplication, Folding, Mid squares, Extraction와
key 값이 string일 때의 Additive, Rotating 등 다양한 해시 함수들이 있다.

해시 테이블의 평균 데이터 처리의 시간 복잡도는 O(1)이지만, 이는 해시 함수의 연산을 고려하지 않는 결과
해시 함수가 매우 복잡하다면 해시테이블의 모든 연산의 시간 효율성은 증가
-> 해시 함수의 선택도 중요


충돌 회피 함수 (Hash collision resolution method)

open addressing

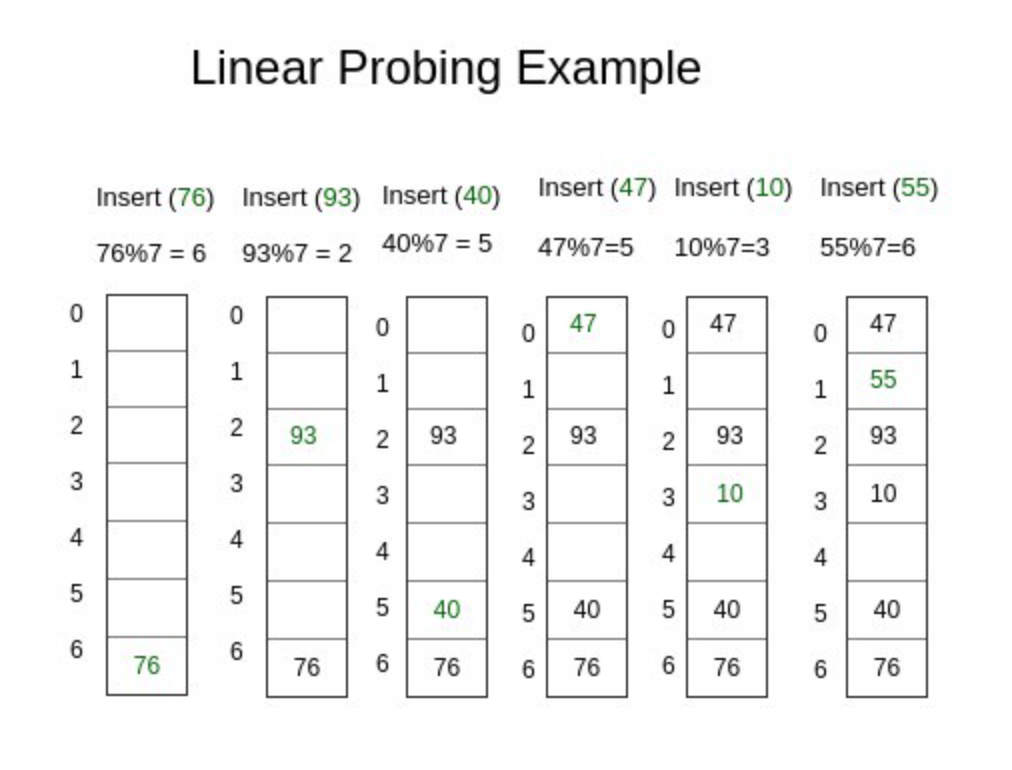
  • linear probing
    • 폐쇄 해싱 또는 Close Hashing 기법 중 하나: 해쉬 테이블 저장공간 안에서 충돌 문제를 해결하는 기법
    • 충돌이 일어나면, 해당 hash address의 다음 address부터 맨 처음 나오는 빈공간에 저장하는 기법
    • 저장공간 활용도를 높이기 위한 기법
    • linear probing으로 충돌을 회피할 때 클러스터(저장된 자료가 모여있는 군집)가 적어야 시간 복잡도가 줄어듦
  • quadratic probing
    • k -> k + 1^2 -> k + 2^2 -> k + 3^2 -> …
  • double hashing
    • 해시 함수를 두개 사용하는 기법
    • f(key) -> f(key) + g(key) -> f(key) + 2g(key) -> f(key) + 3g(key) -> …

장점

  • 또 다른 저장공간 없이 해시테이블 내에서 데이터 저장 및 처리가 가능
  • 또 다른 저장공간에서의 추가적인 작업이 없음

단점

  • 해시 함수(Hash Function)의 성능에 전체 해시테이블의 성능이 결정됨
  • 데이터의 길이가 늘어나면 그에 해당하는 저장소를 마련해 두어야 함
출처 : https://www.geeksforgeeks.org/
linear probing 예시


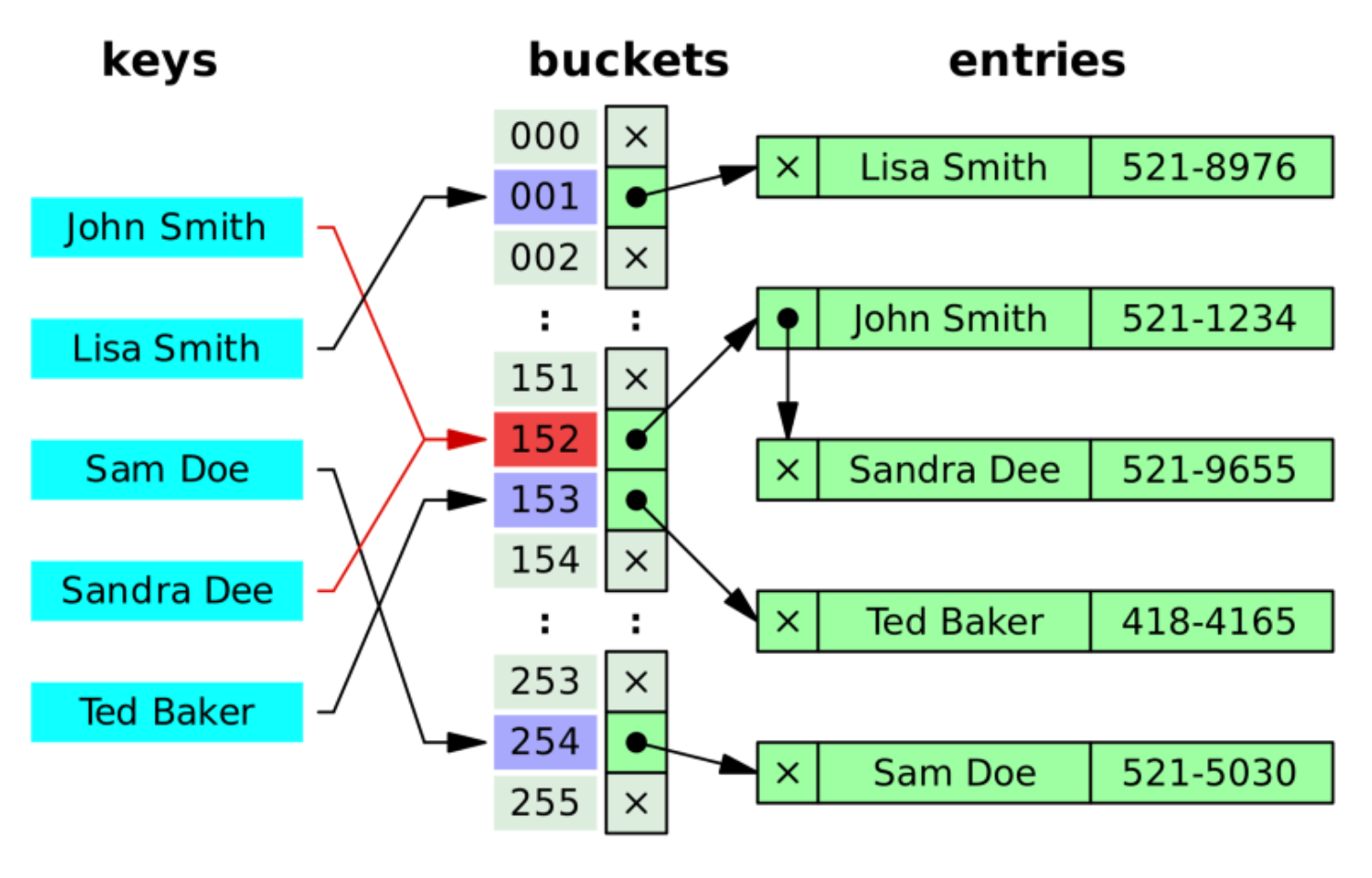
chaining

  • 개방 해싱 또는 Open Hashing 기법 중 하나: 해시 테이블 저장공간 외의 공간을 활용하는 기법
  • 충돌이 일어나면, 링크드 리스트라는 자료 구조를 사용해서, 링크드 리스트로 데이터를 추가로 뒤에 연결시켜서 저장하는 기법

장점

  • 한정된 저장소(Bucket)을 효율적으로 사용 가능
  • 해시 함수(Hash Function)을 선택하는 중요성이 상대적으로 적음
  • 상대적으로 적은 메모리를 사용하여 미리 공간을 잡아 놓을 필요가 없음

단점

  • 한 Hash에 자료들이 계속 연결된다면(쏠림 현상) 검색 효율을 낮출 수 있음
  • 외부 저장 공간을 사용하여 외부 저장 공간 작업을 추가로 해야 함
출처 : https://velog.io/@cyranocoding/
chaining 예시 


class HashTable:
    def __init__(self):
        self.hash_table = list([0 for i in range(8)])
        
    def get_key(self):
        return hash(self)
    
    def hash_function(self, key):
        return key % 8
    
    def insert(self, key, value):
        hash_value = self.hash_function(get_key(data))
        self.hash_table[hash_value] = value
        
    def read(self, key):
        hash_value = self.hash_function(get_key(key))
        return self.hash_table[hash_value]
    
    def print(self):
        print(self.hash_table)
해시 테이블을 파이썬으로 구현


삽입 삭제 탐색 연산은 cluster size에 영향을 받음
cluster size는 해시 함수, 충돌 해결 함수, 로드 팩터의 영향을 받음
(로드 팩터 : (테이블에 저장된 아이템의 갯수) / (슬롯의 갯수))

로드 팩터와 충돌 비율을 통해서 해시 테이블에 관련된 연산들의 수행시간, 성능 등을 평가 가능

클러스터의 빈 슬롯이 평균적으로 50% 이상을 유지한다면 해시 테이블의 연산의 시간 복잡도가 평균 O(1)으로 수렴

참고

잔재미코딩
신찬수 교수님 유튜브



© 2021. by hminkim