[Data Structure] Tree
Tree 트리
- 일반적으로 대상 정보의 각 항목들을 계층적으로 연관되도록 구조화시키고자 할 때 사용하는 비선형 자료구조
- Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 한 개의 루트 노드만이 존재하며, 모든 자식 노드는 한 개의 부모 노드만을 가짐 (즉, 루트에서 어떤 노드로 가는 경로는 유일)
- 보통 이진 트리(Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
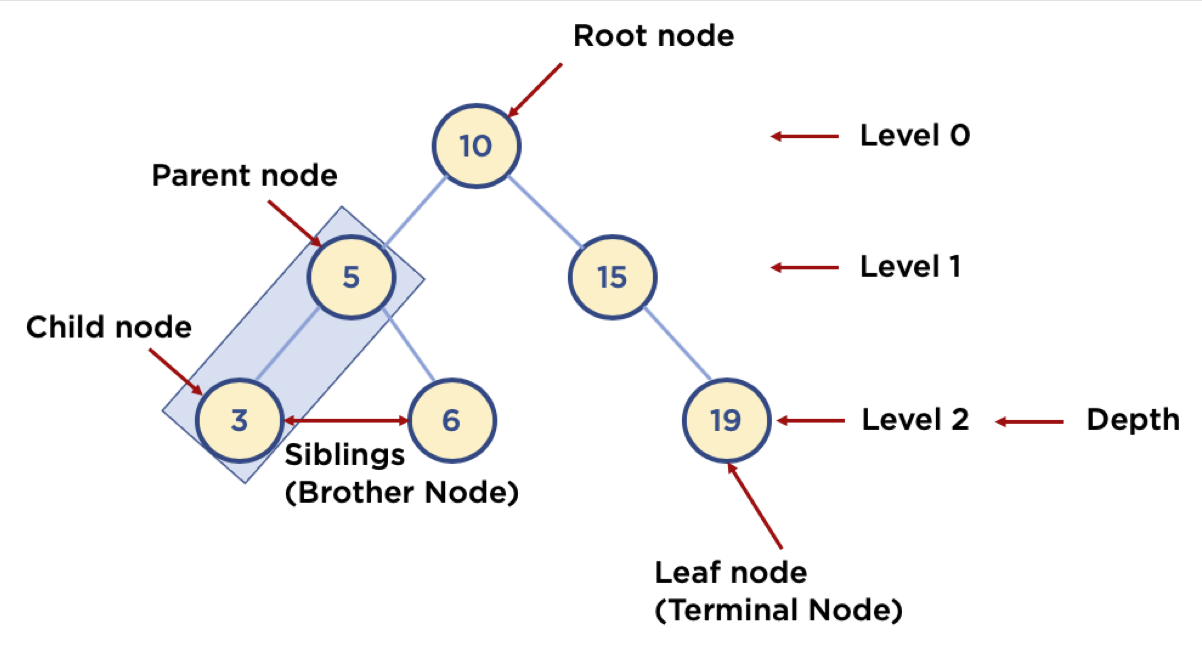
트리 관련 용어
- 노드 (Node) : 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- 간선 (Branch) : 노드를 연결하는 선 (edge, link라고도 부름)
- 내부 노드 (Internal Node) : 말단 노드가 아닌 노드
- 루트 노드 (Root Node) : 트리 맨 위에 있는 노드
- 말단 노드 (Leaf Node) : 자식 노드가 하나도 없는 노드 (단말 노드, 잎 노드)
- 부모 노드 (Parent Node) : 어떤 노드의 다음 레벨에 연결된 노드
- 자식 노드 (Child Node) : 어떤 노드의 하위 레벨에 연결된 노드
- 형제 노드 (Brother Node) : 동일한 부모 노드를 가진 노드 (Sibling)
- 노드의 레벨 (Level): 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- 노드의 크기 (Size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이 (Depth) : 트리에서 노드가 가질 수 있는 최대 레벨
- 노드의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
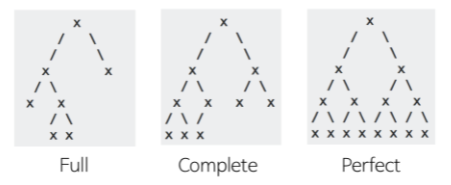
트리의 종류
- 이진 트리 (Binary Tree) : 노드의 최대 Branch가 2인 트리
- 완전 이진 트리 (Complete Binary Tree) : 노드를 삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리
- 전 이진 트리 (Full Binary Tree) : 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
- 포화 이진 트리 (Perfect Binary Tree) : 모든 내부 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는 트리
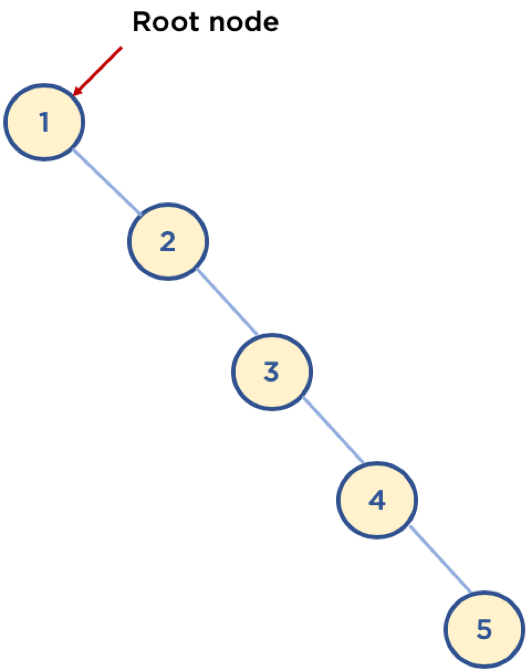
- 편향 트리 (Skewed Tree) : 한쪽으로 기울어진 트리, 사향 트리라고도 부름
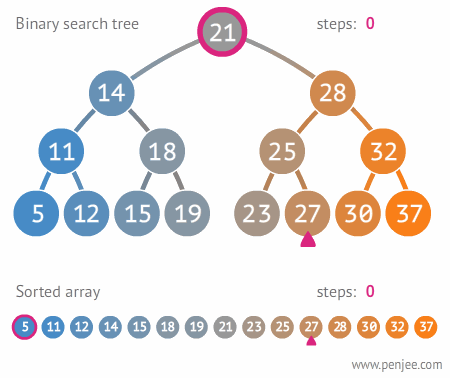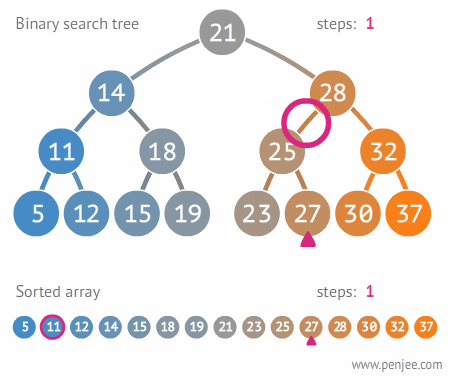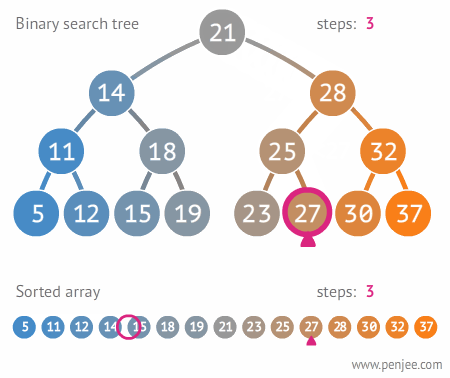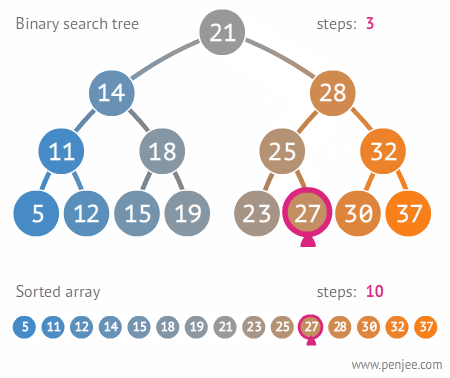
이진 탐색 트리 (Binary Search Tree, BST)
왼쪽 노드는 해당 노드보다 작거나 같은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지는 추가적인 조건이 있는 이진 트리

이진 탐색 트리의 시간 복잡도
- 트리의 높이를 h라고 표현 한다면, O(h)의 시간 복잡도를 가짐
- n개의 노드를 가진다면, h = logn에 가까우므로 시간 복잡도는 O(logn)
장점
- 기존의 O(n)의 탐색 속도를 O(logn)으로 개선할 수 있음
단점
- 균형이 잡혀 있을 때 기준 시간복잡도는 O(logn)이지만 편향 트리에서는 링크드 리스트등과 동일한 성능을 보여줄 수도 있음
- 이를 해결하기 위해 균형 이진 탐색 트리를 활용 함
# 노드 클래스 만들기
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BST:
def __init__(self, head):
self.head = head
# 데이터 삽입
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
# 데이터 탐색
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
return False
#데이터 삭제
def delete(self, value):
# 삭제할 노드 탐색
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value:
searched = True
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:
return False
# case1 : 삭제할 노드가 Leaf Node일 경우
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None
else:
self.parent.right = None
# case2 : 삭제할 노드가 Child Node를 한 개 가지고 있을 경우
elif self.current_node.left != None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
elif self.current_node.left == None and self.current_node.right != None:
if value < self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right
# case 3 - 삭제할 노드가 Child Node를 두개 가지고 있을 경우
elif self.current_node.left != None and self.current_node.right != None:
# case3-1 : 삭제할 Node가 Parent Node 왼쪽에 있을 때
if value < self.parent.value:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.change_node.left
# case 3-2 : 삭제할 Node가 Parent Node 오른쪽에 있을 때
else:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.left
return True
균형 이진 탐색 트리 (Balanced BST)
평균적으로 O(logn)의 연산 속도를 가진 이진 검색 트리가 편향 트리가 되었을 때 O(n)의 연산 속도를 가지는 것을 방지하기 위해 만들어진 자료구조
Red-Black 트리
- 아래 5가지 조건을 가지는 이진 탐색 트리
- 트리의 모든 노드는 Red or Black으로만 구성되어 있음
- 루트 노드는 무조건 Black
- 모든 리프 노드는 무조건 Black
- 루트 노드에서 리프 노드까지 Black의 갯수는 항상 같음
- Red 노드의 자식은 모두 Black (Black 노드의 자식은 상관 없음)
- 자바에서는 treeSet, treeMap이 Red-Black 트리를 구현함
5번 조건으로 인해 Red는 중복될 수 없으니 Red와 Red 사이엔 하나의 블랙 노드를 끼게 되고, 이는 곧 Red-Black 트리의 총 깊이가 됨
결국 블랙 노드만을 가지는 가장 짧은 깊이와 Red-Black의 차이는 무조건 2배 이하의 길이 차이가 남
AVL 트리
- 모든 노드에 대해서 노드의 왼쪽부 트리와 오른쪽부 트리의 높이 차가 1 이하로 맞춘 이진 탐색 트리
- -1, 0, 1로 이루어진 Balance Factor를 기준으로 Rotation이 이루어져 균형을 맞춤
Red-Black vs AVL
- 더 엄격한 균형을 유지하고 있는 AVL이 Red-Black보다 더 빠른 Search 속도를 제공
- 더 느슨한 균형을 유지하고 있는 Red-Black이 AVL보다 더 빠른 Insert와 Delete 속도를 제공
- Red-Black은 대부분의 언어 라이브러리에서 자주 사용
- AVL은 조회에 자주 사용되는 Database에 자주 사용
