[Algorithm] Divide and conquer
in Computer Science on Algorithm
Divide and conquer 분할 정복
- 분할정복법은 주어진 문제를 작은 사례로 나누고 각각의 작은 문제들을 해결하여 정복 (Conquer)하는 방법
- 분할 정복 패러다임을 차용한 알고리즘들은 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산, 각 부분 문제의 답으로부터 전체 문제의 답을 계산
- 주로 재귀함수를 이용하여 구현하는 것이 일반적이나, 재귀호출을 사용하지 않고 스택, 큐 등의 자료구조를 이용하여 구현하기도 함
- 대표적인 분할 정복법을 활용한 알고리즘으로는 퀵 정렬과 병합 정렬이 있음
분할 정복 프로세스
- Divide (분할) : 문제를 동일한 유형의 여러 하위 문제로 분할
- Conquer (정복) : 가장 작은 단위의 하위 문제들을 해결하며 정복
- Combine (조합) : 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합
문제를 제대로 분할하면 정복하는 것은 쉽기 때문에 제대로 분할하는 것이 중요
분할 정복법은 재귀 호출이 자주 사용되는데, 이 부분에서 분할 정복법의 효율성이 떨어질 수도 있음
분할 정복의 장단점
장점
- 문제를 나누어 해결함으로써 어려운 문제를 보다 쉽게 해결할 수 있음
- 문제를 나누어 해결한다는 특징상 병렬적으로 문제를 해결하는 데 큰 강점이 있음
단점
- 함수를 재귀적으로 호출하게 되면 함수 호출로 인한 오버헤드가 발생하며, 스택에 다양한 데이터를 보관하고 있어야 하므로 스택 오버플로우가 발생하거나 과도한 메모리 사용을 하게 됨
분할 정복 vs 재귀 호출
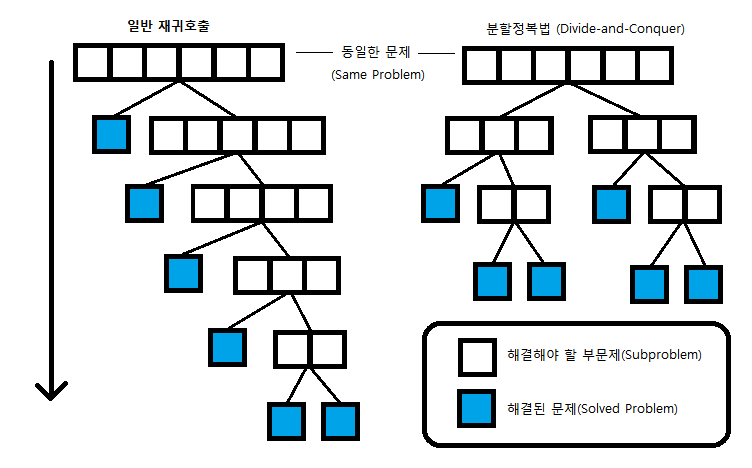
- 일반적인 재귀 호출과의 차이점은 항상 문제를 한 조각과 나머지로 쪼개는 방식인 재귀 호출과는 달리 분할정복법은 항상 문제를 절반씩으로 나누어 문제를 해결
분할 정복 vs 동적 계획법
- 문제를 잘게 쪼개서, 가장 작은 단위로 분할하여 문제를 해결한다는 공통점이 있음
- 동적 계획법은 중복되는 부분이 없는 분할 정복과는 다르게 Memoization 기법을 사용하여 부분 문제는 중복되며, 상위 문제 해결 시 재활용될 수 있음 (부분 문제의 해답을 저장해서 재활용하는 최적화 기법으로 사용)
참고
잔재미코딩
신찬수 교수님 유튜브
Cristoval Blog
나무 위키
