[Algorithm] Dynamic Programing

in Computer Science on Algorithm


Dynamic Programing 동적 계획법

  • 특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법
  • Dynamic이라는 이름과는 다르게 전혀 동적이진 않은데 이는 처음 이 방식을 사용한 벨만이 다른 이유 없이 Dynamic 이라는 단어가 그저 멋있어서 선택했다고 함
  • 분할 정복과는 다르게 동적 계획법은 두가지 전제 조건이 있어야 동적 계획법으로 문제를 해결 가능
    1. Overlapping Subproblem : 겹치는 작은 문제
      • 어떤 문제가 여러개의 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀를 통해 해결되는 부분 문제로 쪼개질 수 있을 때
    2. Optimal Substructure : 최적 부분구조
      • 어떤 문제의 최적의 해결책이 그 부분 문제의 최적의 해결책으로 부터 설계될 수 있을 때, 즉, 최적 부분구조 일때 문제의 정답을 작은 문제의 정답에서 부터 구할 수 있음
      • 이 속성은 동적 계획법이나 그리디 알고리즘의 유용성을 판별하는데 사용되기도 함

Memoization 메모이제이션

  • 동일한 문제를 반복해야 할 경우, 한 번 계산된 결과를 저장해 두었다가 활용하는 방식으로 중복 계산을 줄이는 것
  • 동적 계획법을 분할 정복과 나누는 가장 큰 차이점 중 하나

출처 : https://coding-all.tistory.com/2
중복 제거 전(왼쪽)과 후(오른쪽) 시간복잡도 변화


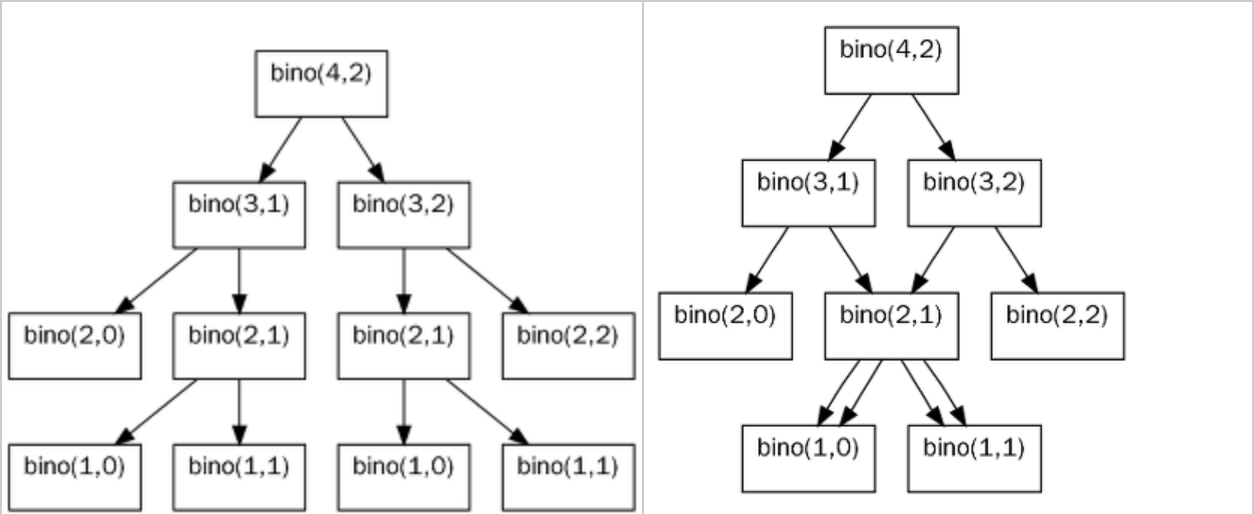
동적 계획법 구현 방식

Top-down 방식

  • 큰 문제부터 시작해서 작은 문제로 분할해 가면서 풀어 나가는 방식 (위에서 아래로 진행)
  • 함수 호출을 줄이기 위해 메모이제이션 방식을 활용
  • 재귀로 구현
  • 장점
    • 좀 더 직관적인 코드를 구현 가능
    • 부분 문제 간의 의존 관계나 계산 순서에 대해 고민할 필요 없음
    • 전체 부분 문제 중 일부의 답만 필요할 경우 더 빠르게 동작
  • 단점
    • 함수가 return 값을 반환해야 스택이 비워지는데, 재귀함수를 사용하면 호출시 마다 함수가 끝나지 않은 도중에 계속 함수가 호출됨으로 함수의 깊이는 계속 깊어만 지고, 계속 메모리가 쌓이게 되어서 stack overflow가 일어날 수 있음

Bottom-up 방식

  • 작은 문제들을 쌓아 올려 큰 문제를 풀어 나가는 방식 (아래에서 위로 진행)
  • 반복문으로 구현
  • 장점
    • 보통 더 짧은 코드로 구현 가능
    • 재귀 호출에 필요한 부하가 없기 떄문에 일반적으로 더 빠르게 동작
  • 단점
    • 좀 더 구현된 코드가 비직관적
    • 부분 문제 간의 의존 관계를 고려해 계산되는 순서를 고려해야 함

Top-down과 Botton-up의 시간복잡도 차이는 문제에 따라 다를 수 있으므로 정확히 알 수는 없음
Top-down은 재귀호출을 하기때문에 스택의 사용으로 시간이 더 걸릴 수 있지만, 실제로 그 차이는 크지 않음
다만, 파이썬의 경우 재귀 호출 시 stack overflow가 발생할 수 있기때문에, Bottom-up으로 구현하는 것이 좋음 (C++과 JAVA에서는 재귀로 구현하는 것이 크게 문제가 되지 않음)


def fibonacci(n):
    if n < 2:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

def fibonacci_arr(n):
    arr = []
    for i in range(n+1):
        arr.append(fibonacci(i))
    return arr
피보나치 수열을 일반 재귀로 구현 


def fibonacci(n):
    if n < 2:
        return n
    else:
        fibo = fibonacci(n - 1) + fibonacci(n - 2) # Memoization
    return fibo

def fibonacci_arr(n):
    arr = []
    for i in range(n+1):
        arr.append(fibonacci(i))
    return arr
피보나치 수열을 Top-down 방식 (재귀함수)으로 구현 


def fibonacci(n):
    arr = []
    for i in range(0,n+1):
        if i < 2:
            arr.append(i)
        else:
            arr.append(arr[i-1] + arr[i-2])
    return arr
피보나치 수열을 Bottom-up 방식 (반복문)으로 구현


동적 계획법 vs 그리디 알고리즘

  • 모든 방법을 일일이 검토하여 최적의 해를 찾아내는 방식의 동적 계획법과 달리, 그리디 알고리즘은 모든 해를 구하지 않고 순간마다 그 순간에서의 최적의 해를 찾는 방식
  • 그리디 알고리즘은 닥치는 순간만을 고려해서 해를 구하기 때문에 도출된 값이 항상 최적의 해라고 할 수는 없지만 동적 계획법은 모든 방법을 검토해 보고 결과적으로 효율적인 값 도출
  • 일반적으로 동적 계획법은 그리디 알고리즘에 비해 시간이 좀 더 걸리지만, 결과적으로는 항상 최적의 해를 구할 수 있다는 이점을 가지고 있음


참고

잔재미코딩
신찬수 교수님 유튜브
위키백과
나무위키
All About Coding Blog
Polynomeer Blog



© 2021. by hminkim