[Algorithm] BFS / DFS

in Computer Science on Algorithm


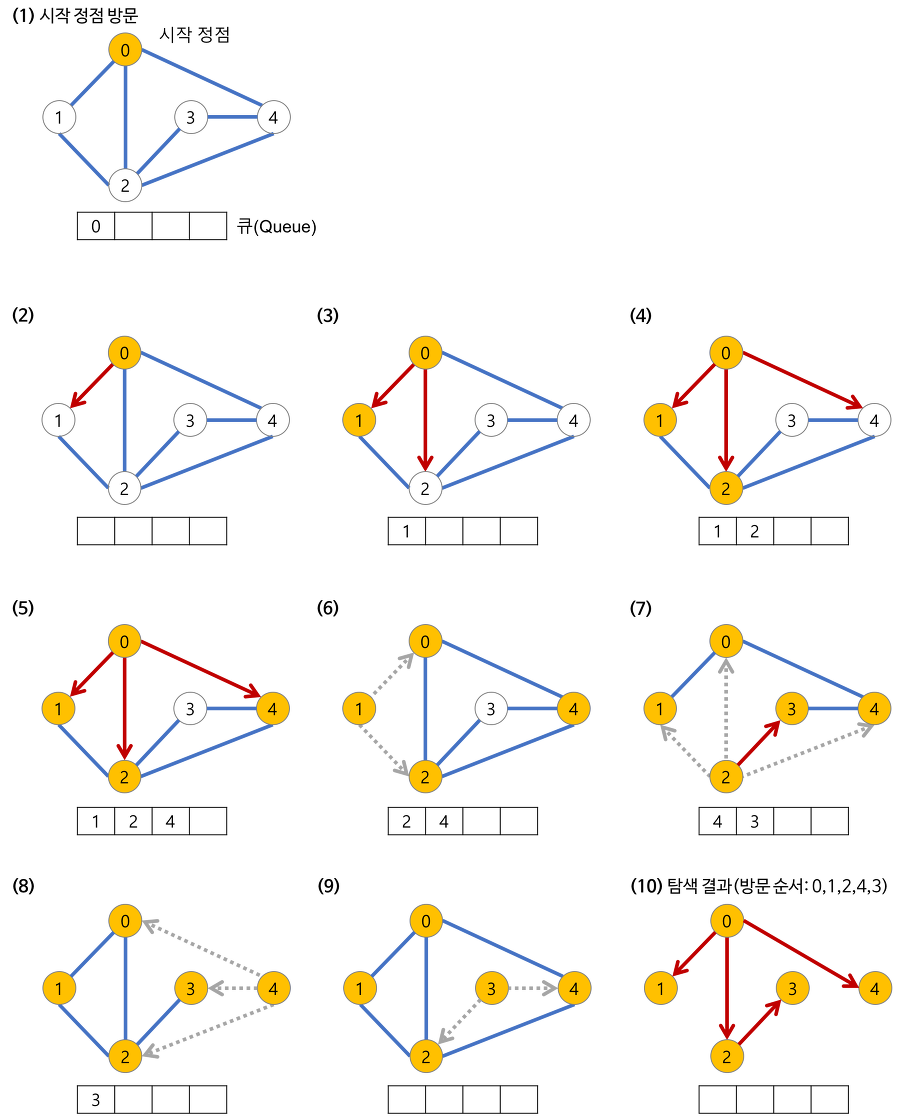
BFS (Breadth First Search) 너비 우선 탐색

  • 정점들과 같은 레벨에 있는 노드들(형제 노드들)을 먼저 탐색하는 방식
  • 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함
  • 주로 queue를 활용하여 구현함

BFS 프로세스

  • 깊이가 1인 모든 노드를 방문하고 나서 그 다음에는 깊이가 2인 모든 노드를, 그 다음에는 깊이가 3인 모든 노드를 방문하는 식으로 계속 방문하다가 더 이상 방문할 곳이 없으면 탐색을 마침


출처 : https://yunyoung1819.tistory.com/86
BFS 프로세스


BFS 구현


출처 : https://www.fun-coding.org/Chapter18-bfs-live.html/
BFS 예시 


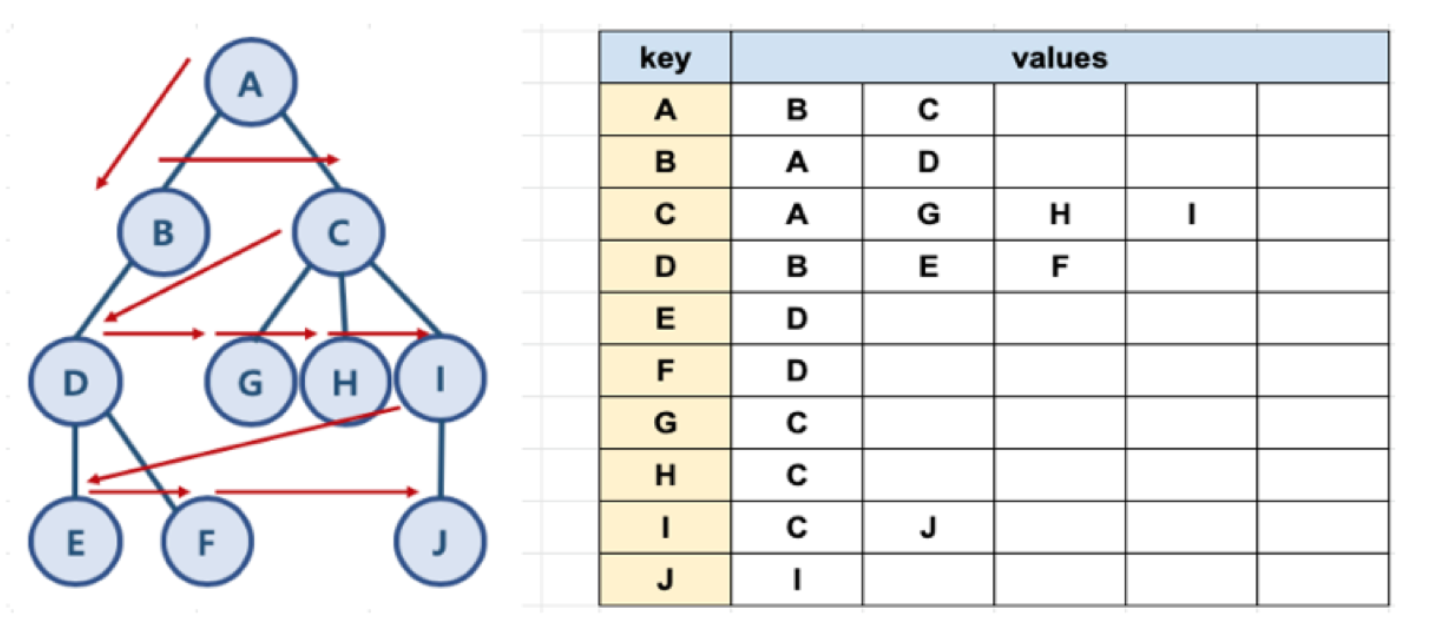
from collections import deque

graph = {
    'A' : ['B', 'C'],
    'B' : ['A', 'D'],
    'C' : ['A', 'G', 'H', 'I'],
    'D' : ['B', 'E', 'F'],
    'E' : ['D'],
    'F' : ['D'],
    'G' : ['C'],
    'H' : ['C'],
    'I' : ['C', 'J'],
    'J' : ['I']
}

def bfs(graph, start_node):
    visited = list()
    queue = deque()
    queue.append(start_node)
    
    while queue:
        node = queue.popleft()
        if node not in visited:
            visited.append(node)
            queue.extend(graph[node])
    
    return visited
BFS를 queue를 활용하여 파이썬으로 구현


  • 시간 복잡도가 O(n)인 list.pop()대신 collection 라이브러리의 deque의 queue.popleft()를 사용함

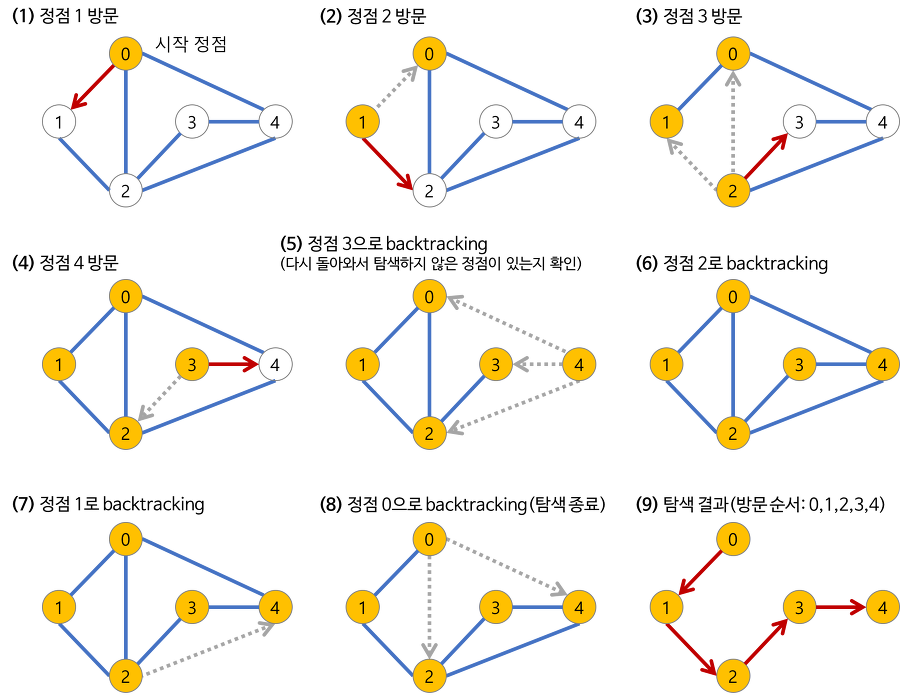
DFS (Depth First Search) 깊이 우선 탐색

  • 정점의 자식들을 먼저 탐색하는 방식
  • 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
  • 주로 재귀 혹은 Stack을 활용하여 구현함

DFS 프로세스

  • 하나의 정점으로부터 시작하여 차례대로 모든 자식 노드들을 우선으로 방문하다가 더 이상 방문할 곳이 없으면 탐색을 마침


출처 : https://yunyoung1819.tistory.com/86
DFS 프로세스


DFS 구현


출처 : https://www.fun-coding.org/Chapter18-bfs-live.html/
DFS 예시 


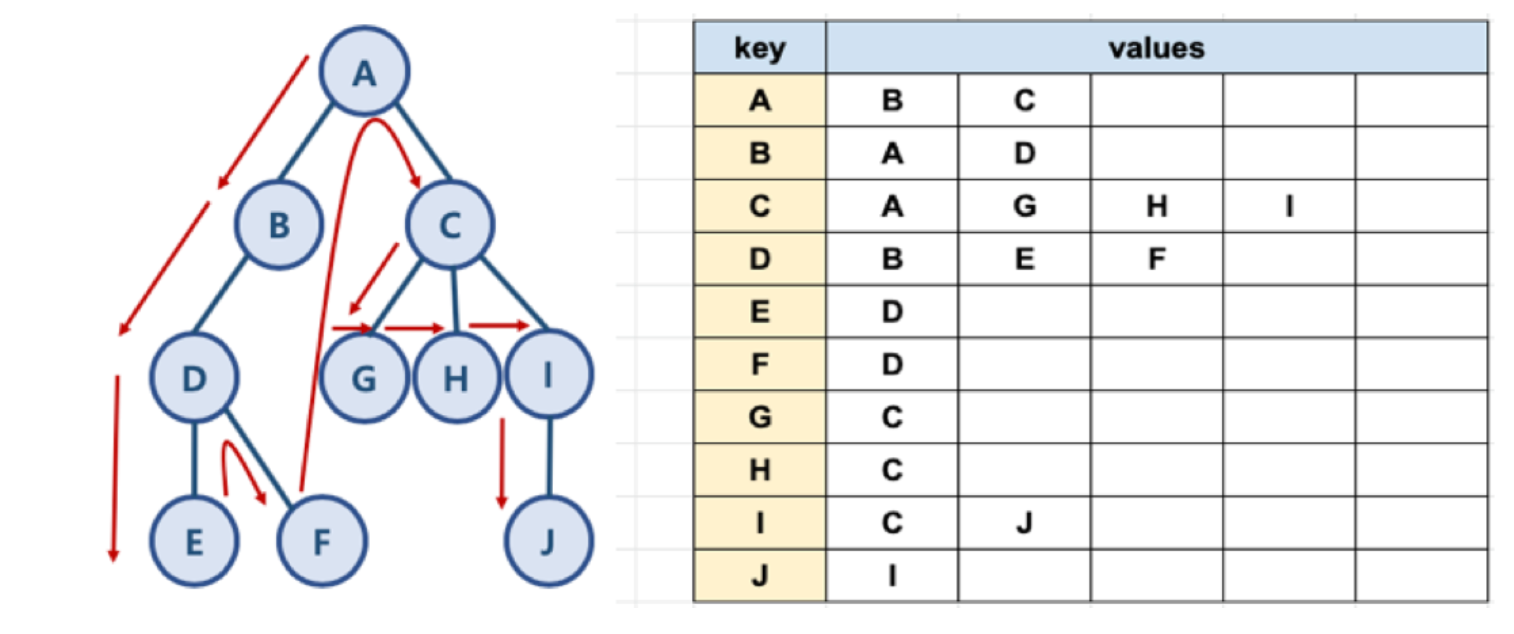
graph = {
    'A' : ['B', 'C'],
    'B' : ['A', 'D'],
    'C' : ['A', 'G', 'H', 'I'],
    'D' : ['B', 'E', 'F'],
    'E' : ['D'],
    'F' : ['D'],
    'G' : ['C'],
    'H' : ['C'],
    'I' : ['C', 'J'],
    'J' : ['I']
}

# stack을 활용한 DFS
def dfs(graph, start_node):
    visited = list()
    stack = list()
    stack.append(start_node)
    
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.append(node)
            stack.extend(sorted(graph[node], reverse = True))
    
    return visited

# 재귀를 활용한 DFS
def dfs_recursive(graph, start_node, visited=[]):
    visited.append(start_node)

    for next_node in graph[start_node]:
        if next_node not in visited:
            dfs_recursive(graph, next_node, visited)
            
    return visited
DFS를 stack과 재귀를 활용하여 파이썬으로 구현


BFS vs DFS


출처 : https://namu.wiki/w/BFS
BFS vs DFS


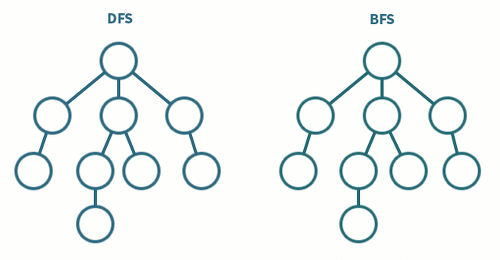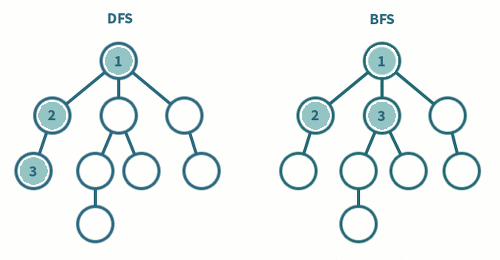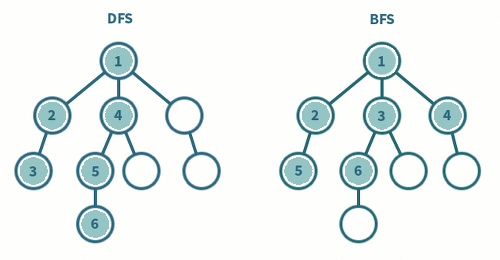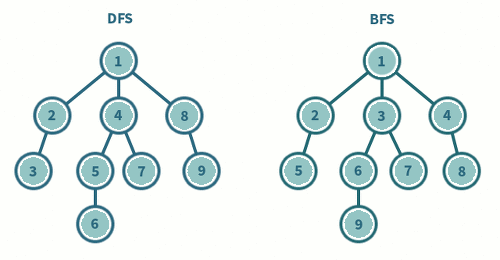
  • 그래프의 모든 정점을 방문하는 것이 주요한 문제
    • 단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용해도 무관
  • 경로의 특징을 저장해둬야 하는 문제
    • 예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용 (BFS는 경로의 특징을 가지지 못함)
  • 최단거리 구해야 하는 문제
    • 미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리
    • 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만, 너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문
  • 검색 대상 그래프의 규모가 크다면 DFS를 고려
  • 검색 대상의 규모가 작고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS가 유리
  • 검색 속도 자체는 DFS가 BFS에 비해 비교적 느림

BFS와 DFS의 시간복잡도

  • 일반적인 BFS와 DFS의 시간 복잡도
    • 노드 수 : V / 간선 수 : E
    • 시간 복잡도: O(V + E)


참고

잔재미코딩
신찬수 교수님 유튜브
나무 위키
튜나 개발일기
_3juhwan.log
Yun Young’s Programming Blog



© 2021. by hminkim