[Algorithm] Backtracking
in Computer Science on Algorithm
Backtracking 백트래킹
- 정답을 찾는 도중 정답의 조건에서 벗어난다면 다른 가능성으로 되돌아가서 정답을 찾아가는 기법
- 가능한 모든 방법을 탐색하는 완전 탐색의 일종이지만 가지치기를 통해 비효율적인 경로를 배제하고 탐색하기에 가지치기의 효율에 따라 효율성 극대화
- 트리 구조를 기반으로 DFS로 깊이 탐색을 진행하면서 각 루트에 대해 조건이 부합하는지 확인(Promising)하고 만약 해당 트리에서 조건에 맞지 않는 노드는 더 이상 탐색을 진행하지 않고 가지를 쳐버림(Pruning)
- 주로 재귀 혹은 스택을 통한 DFS로 구현
- 유망성 검토 (Promising) 후 조건에 부합하지 않으면 가지치기(Pruning)를 통해 다른 자손 노드를 탐색함으로서 풀이시간 단축
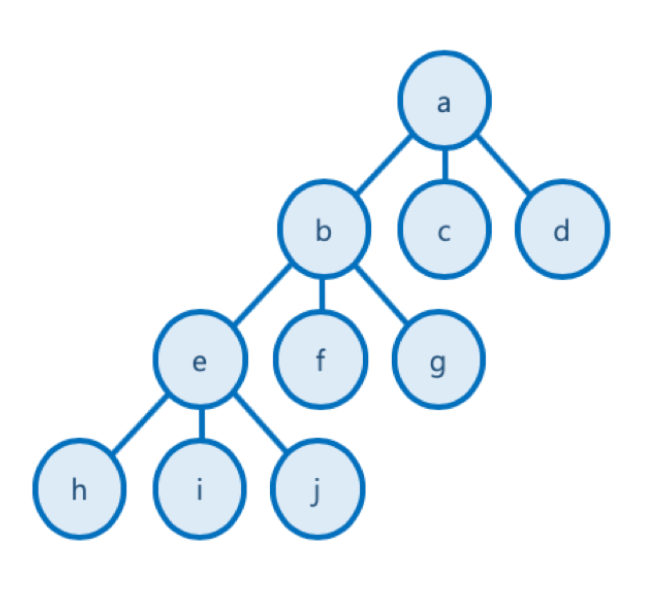
State Space Tree 상태 공간 트리
- 실제 구현 시 고려할 수 있는 모든 경우의 수를 상태 공간 트리(State Space Tree)를 통해 표현
N-Queen 문제
- N x N 크기의 체스판에 가로,세로,대각선으로 어느 위치든 이동할 수 있는 퀸을 서로 공격할 수 없는 위치로 최대한 많이 배치하는 대표적인 백트래킹 문제
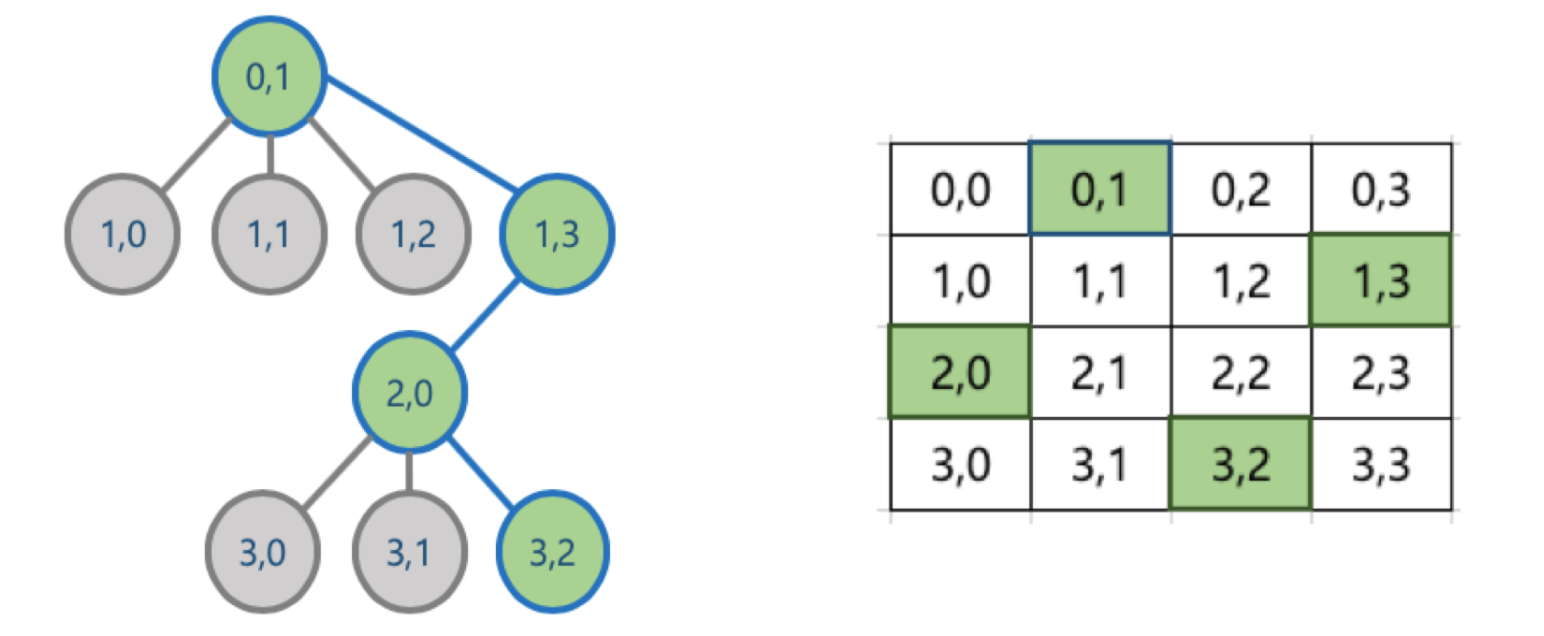
N-Queen 문제 해결 로직
- 퀸은 수평 이동이 가능하므로 한 행에는 하나의 퀸 밖에 위치할 수 없음
- 맨 위에 있는 행부터 퀸을 배치하고, 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치
- 만약 앞선 행에 배치한 퀸으로 인해, 다음 행에 해당 퀸들이 이동할 수 없는 위치가 없을 경우에는, 더 이상 퀸을 배치하지 않고, 이전 행의 퀸의 배치를 바꿈
- 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후, 각 경우를 맨 위의 행부터 DFS 방식으로 접근
- 해당 경우가 진행이 어려울 경우, 더 이상 진행하지 않고, 다른 경우를 체크
N-Queen 문제 알고리즘 구현
def is_available(candidate, current_col):
current_row = len(candidate)
for queen_row in range(current_row):
if candidate[queen_row] == current_col or abs(candidate[queen_row] - current_col) == current_row - queen_row:
return False
return True
def DFS(N, current_row, current_candidate, final_result):
if current_row == N:
final_result.append(current_candidate[:])
return
for candidate_col in range(N):
if is_available(current_candidate, candidate_col):
current_candidate.append(candidate_col)
DFS(N, current_row + 1, current_candidate, final_result)
current_candidate.pop()
def solve_n_queens(N):
final_result = []
DFS(N, 0, [], final_result)
return final_result
