Union-Find Algorithm 유니온 파인드 알고리즘

• 대표적 그래프 알고리즘으로 합집합 찾기 라는 의미를 가지고 있음
• 주어지는 개체들이 중복된 값을 가지지 않는 별개의 개체들 즉, 집합들간에 교집합이 없는 집합을 상호배타적 집합(Disjoint Set) 또는 서로소 집합이라 할 수 있는데 이런 문제를 풀 때 사용되는 알고리즘으로 주요 연산의 이름에서 따와 Union-find 알고리즘이라 부름
• 여러 노드가 존재할 때 두개의 노드를 선택해서 현재 두 노드가 서로 같은 그래프에 속하는지 판별하고 두개의 노드를 같은 집합으로 묶어주는 알고리즘
  • make-set : n 개의 원소가 개별 집합으로 이뤄지도록 초기화
  • Union : 두 개별 집합을 하나의 트리로 합치는 연산
  • Find : 두 개의 노드를 선택해서 서로 같은 그래프에 속하는지 판별하기 위해 각 그룹의 루트 노드를 확인

Union-Find 알고리즘 로직

• Union 순서에 따라서, 최악의 경우 완전 비대칭 형태의 트리인 링크드 리스트와 같은 형태가 될 수 있음
• Find-Union 시 시간복잡도가 O(n) 이 될 수 있으므로, 해당 문제를 해결하기 위해, union-by-rank, path compression 기법을 사용함
  
  

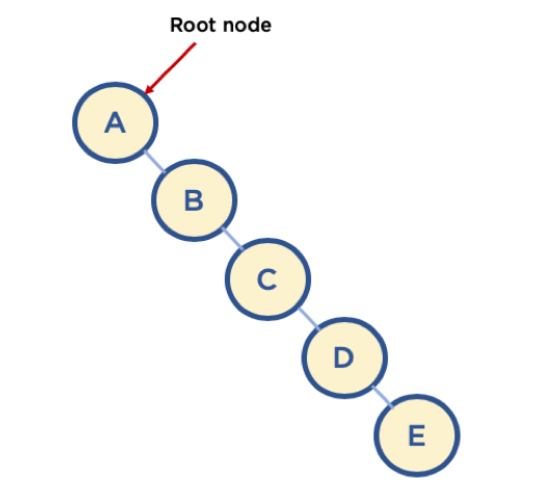
make-set 초기화

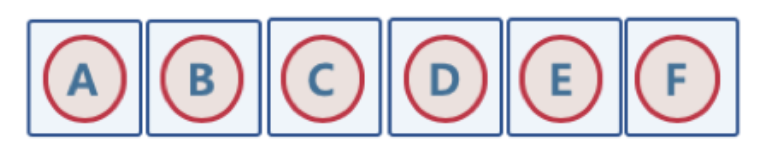
Union 연산

• Union-by-rank 기법
  • 각 트리에 대해 높이(rank)를 기억해 두고, Union시 두 트리의 높이(rank)가 다르면, 높이가 작은 트리를 높이가 큰 트리에 붙임 (즉, 높이가 큰 트리의 루트 노드가 합친 집합의 루트 노드가 되게 함)
    
    
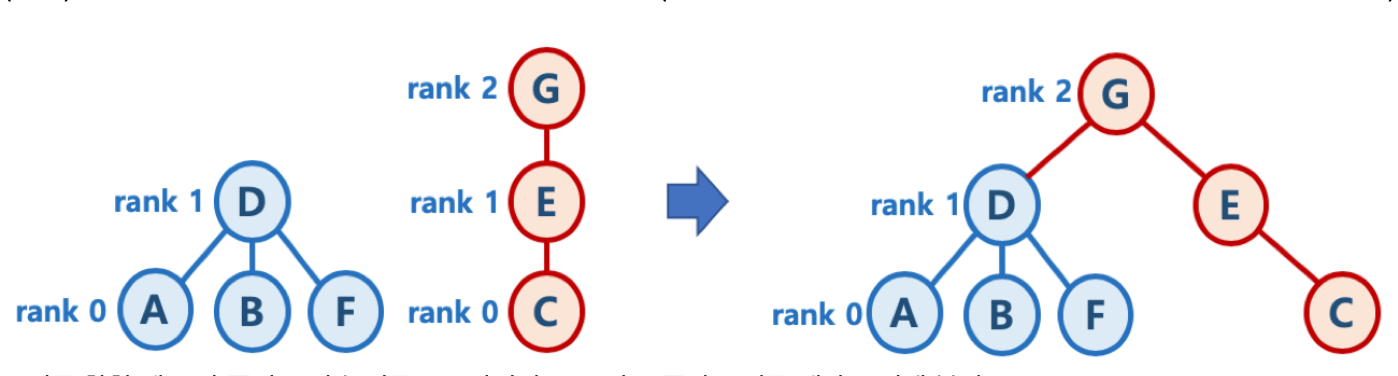
  출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 두개의 트리 높이가 다를 때의 union 연산

  
  

  • 높이가 같은 두 개의 트리를 합칠 때는 한 쪽의 트리 높이를 1 증가시켜주고, 다른 쪽의 트리를 해당 트리에 붙여줌
    
    
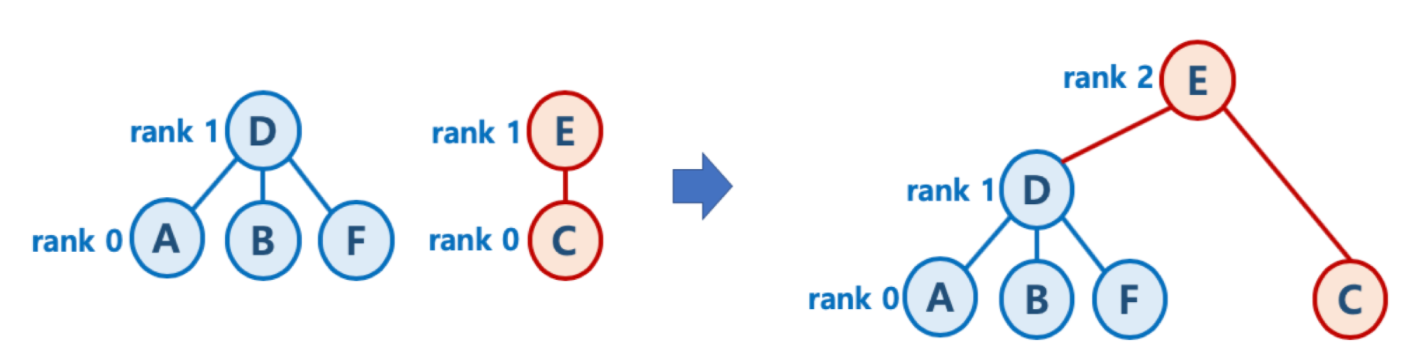
  출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 두개의 트리 높이가 같을 때의 union 연산

  
  

  • 초기화시, 모든 원소는 높이(rank) 가 0 인 개별 집합인 상태에서, 하나씩 원소를 합칠 때, union-by-rank 기법을 사용한다면,
    • 높이가 h 인 트리가 만들어지려면, 높이가 h - 1 인 두 개의 트리가 합쳐져야 함
    • 높이가 h - 1 인 트리를 만들기 위해 최소 n개의 원소가 필요하다면, 높이가 h 인 트리가 만들어지기 위해서는 최소 2n개의 원소가 필요함
    • 따라서 union-by-rank 기법을 사용하면, union-find 연산의 시간복잡도는 O(n) 이 아닌, O(logn)으로 낮출 수 있음

Find 연산

• Path compression 기법
  • Find를 실행하는 과정 가운데에서 경로 상의 모든 노드들을 곧바로 루트 노드 아래에 달아주는 최적화
    
    
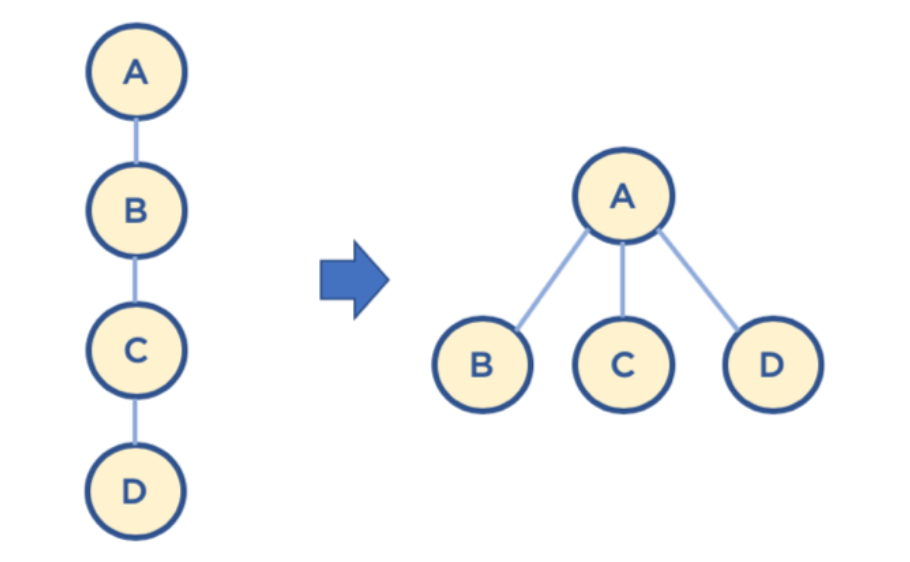
  출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html Path compression 연산

  
  

Union-find 알고리즘 구현

def make_set(node):
    parent[node] = node
    rank[node] = 0

def find(node):
    # path compression 기법
    if parent[node] != node:
        parent[node] = find(parent[node])
    return parent[node]

def union(node_v, node_u):
    root1 = find(node_v)
    root2 = find(node_u)
    
    # union-by-rank 기법
    if rank[root1] > rank[root2]:
        parent[root2] = root1
    else:
        parent[root1] = root2
        if rank[root1] == rank[root2]:
            rank[root2] += 1

Union-find 알고리즘 시간 복잡도

• Path compression 기법만을 사용하였을 때, m번의 find 연산을 수행하였다고 가정할 때, 평균 시간 복잡도는 O(mlogn)이나 완전 비대칭 형태의 트리 형태가 되어 최악의 경우 O(n)의 시간 복잡도가 걸릴 수 있음
• union-by-rank 와 path compression 기법, 두 최적화 기법을 모두 사용시 시간 복잡도는 O(log`N)
  • 조금 더 빠르게 증가하는 함수 log`N은 N에 logN의 연산을 반복해서 N <= 1이 되도록 하는 연산 횟수로 정의
  • 65536 < N <= 2^65536 일 때, log`N = 5를 만족하기에 거의 O(1) 상수 시간에 수렴한다고 봐도 무방
  • 이에 대한 자세한 내용은 굳이 이 포스트에서 다루지 않으려 하니 자세한 내용은 여기참조

참고

잔재미코딩
신찬수 교수님 유튜브
Heee’s Development Blog
삼성SW멤버십 Blog