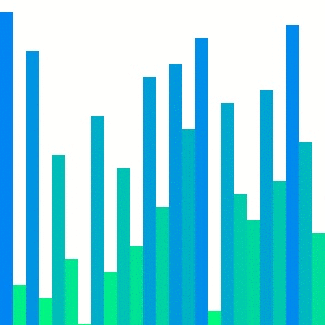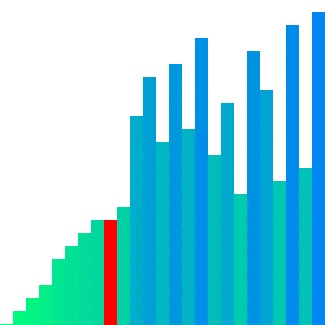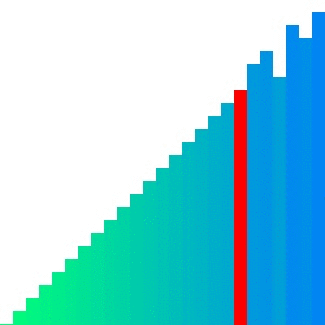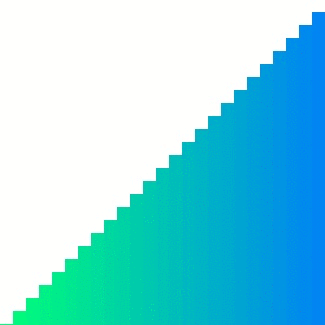Recursion 재귀
- 정의 단계에서 자신을 재참조 하는 함수
- 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식
- 재귀 호출이나 되부름 이라고도 함
Continue reading
Sort Algorithm 정렬 알고리즘
Quick Sort 퀵 정렬
- 기준점(pivot)을 정해서 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right)로 모으는 방식
- 평균적으로 매우 빠른 수행 속도를 내는 정렬 방식
- 분할 정복 알고리즘의 하나로, 재귀 알고리즘을 이용한 정렬 방식
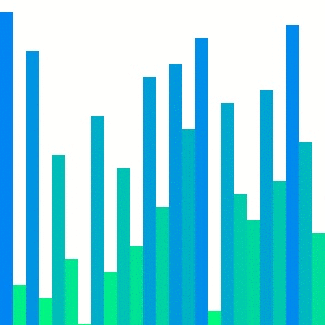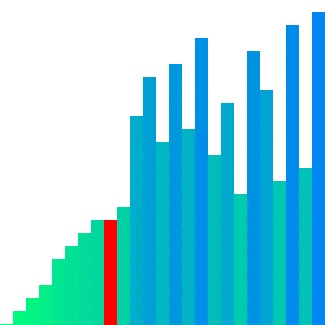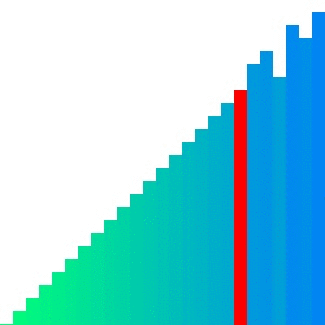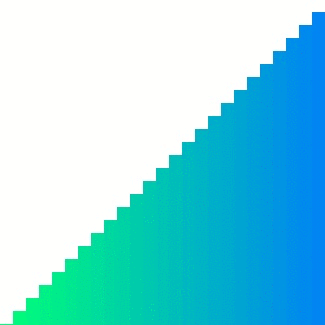 출처 : https://d2.naver.com/helloworld/0315536 퀵 정렬 동작 모습
출처 : https://d2.naver.com/helloworld/0315536 퀵 정렬 동작 모습
동작 원리
- n개의 데이터가 있는 리스트의 첫 번째 데이터를 피벗으로 설정
- 피벗을 기준으로 작은 값과 큰 값을 분류
- 만약 데이터가 피벗보다 작다면
left 리스트에 데이터 추가 - 만약 데이터가 피벗보다 크다면
right 리스트에 데이터 추가
- 리스트의 길이가 1 이하가 될 때 까지
left 리스트와 right 리스트 함수 재귀
```python def quick_sort(data): if len(data) <= 1: return data
Continue reading
Sort Algorithm 정렬 알고리즘
- 어떤 데이터들을 정해진 순서대로 나열하는 것
- 정렬의 목표 : 비교 횟수와 교환 횟수를 최소화
정렬 알고리즘의 성질
- stable sort 안정 정렬 vs unstable sort 불안정 정렬
- 중복된 수의 순서가 유지되는지 안되는지 여부
- Stable Sorting
Bubble Sort 버블 정렬
Insertion Sort 삽입 정렬
Merge Sort 합병 정렬
- Unstable Sorting
Selection Sort 선택 정렬
Heap Sort 힙 정렬
Quick Sort 퀵 정렬
- in-place 제자리 정렬
- 추가적인 메모리 공간을 많이 필요로 하지 않는 혹은 전혀 필요하지 않는 알고리즘을 의미
- 통상적으로, 공간은 O(logn)이고 O(n)이 될 때도 있음
Selection Sort 버블 정렬
Selection Sort 선택 정렬
Insertion Sort 삽입 정렬
Heap Sort 힙 정렬
Quick Sort 퀵 정렬
Bubble Sort 버블 정렬
- 서로 인접한 두 원소를 비교하여 큰 수를 오른쪽으로 하나씩 밀어내어 최댓값을 가장 마지막으로 보내는 정렬
 출처 : https://blog.csdn.net/weixin_42022175/article/details/101203937 버블 정렬 동작 모습
출처 : https://blog.csdn.net/weixin_42022175/article/details/101203937 버블 정렬 동작 모습
Continue reading
날짜: 2021년 7월 12일
소요 시간: 18분 18초
카테고리: 문자열
태그: 레벨1, 파이썬
Continue reading
오랜만에
오랜만에 다시 일기를 끄적이려 새벽감성에 노트북을 켰다. (사실 공부한다고 노트북은 켜져있긴 했다.) 딱히 무언가 딱 떠오르는 글감이 있어서 켰다기 보단 요즘 내가 느끼고 생각하는 것들을 잠시 정리할 필요가 있을 것 같아서 다이어리 포스팅을 하려한다.
취준
나는 대학교 4학년때도 취준 이라는 것을 해본 적이 없는 사람이다. 이미 창업을 통해 취직이 되어 있는 상황 이었고, 기업에 취직 하겠다는 준비 보다는 지금 당장 회사 프로젝트를 어떻게 하면 성공시킬 수 있을 지를 생각했기 때문에 요즘 생에 첫 취준을 하면서 느끼는 바가 정말 많다.
일단 주위 사람들과의 비교에 자존감이 많이 떨어지게 되는 것 같다. 원래 처음 취준을 할 때는 나는 하고싶은 것은 이뤄내야 직성이 풀리는 사람이었고, 사실 1년만에 대기업 갈 수 있을 것 같았다. 학부생 때 열심히 공부한 친구들과 비교해서 나는 열심히 일을 했지 노력의 정도는 같다고 생각했기에 나만 열심히하면 된다는 생각에 취직에 대한 큰 걱정이 없었다. 근데 이게 시간이 지나면 지날 수록 가끔 센치한 밤이면 내가 지금 잘 하고 있는 것인지에 대한 확신이 떨어지면서 가끔 우울해지는 그럴 때가 있다. 주위 취직 잘 해서 열심히 일 하고 차곡차곡 적금도 해가는 친구들과 모아 놓은 돈 오히려 깎아먹으면서 취준 하고 있는 내 모습을 보면서 괜히 비교도 하고 그렇게 되는 것 같다. 남자의 20대 후반 취준 시기가 자존감이 가장 낮을 시기라는 우스갯소리가 마냥 농담 만은 아니구나 하는 걸 최근 조금씩 느끼고 있다.
공부
공부도 그렇고 군대도 그렇고 남들 할 때 해야되는 시기가 있다는 말이 없잖아 맞는 말 처럼 느껴지는 요즘이다. 물론 나는 공부에 시기는 없다고 생각하는 사람이다. 내가 말한 시기의 뜻은 과 동기들이 취준을 할 때 같이 스터디를 하면서 취준을 하면 지금 나 처럼 혼자 공부하는 것 보다는 보다 수월 했지 않았을까 하는 생각에 하는 말이다. 취준 공부를 시작하겠다고 마음을 먹고 서너달은 어떻게 공부해야할 지 방향도 못잡고 그냥 닥치는대로 공부를 했던 것 같다. 뭘 공부해야할지도 모르겠고 어떤 공부를 해야할지도 모르겠어서 갈피를 못잡고 있는 상태로 주위 친구들의 조언, 유튜브, 구글링을 통해서 점점 취준 방향을 잡아나갔다.
거의 비전공자나 다름없는 제로베이스에서 학교 커리큘럼따라 혼자 유튜브 인강, 테크블로그 등을 찾아가며 공부하는 것도 이제 어느정도 익숙해 져서 점점 재미를 붙여가면서 공부하는 중이다. 학생때는 괜히 공부라고 하면 시험이라는 압박과 괜시리 부정적인 느낌에 하기싫고 그랬었는데, 요즘은 압박없이 혼자 정말 지식을 쌓는다는 느낌으로 공부를 하고 있으니 시너지가 좀 더 나는 것 같다. 내 평생 내 입으로 공부가 재밌어서 하고있다는 말을 하게 될 줄 몰랐는데, 요즘엔 조금 그런 느낌도 없잖아 드는 중이다.
Continue reading
Graph 그래프
- 노드와 간선으로 이루어진 노드간의 관계를 표현하는 자료구조
- G = (v,e)로 표현 (v = vertex set / e = edge set)
- 연결되어 있는 객체 간의 조직도를 표현할 수 있는 자료구조
- 지하철 노선도, 도심의 도로 등 실생활에서 다양한 예를 표현 가능
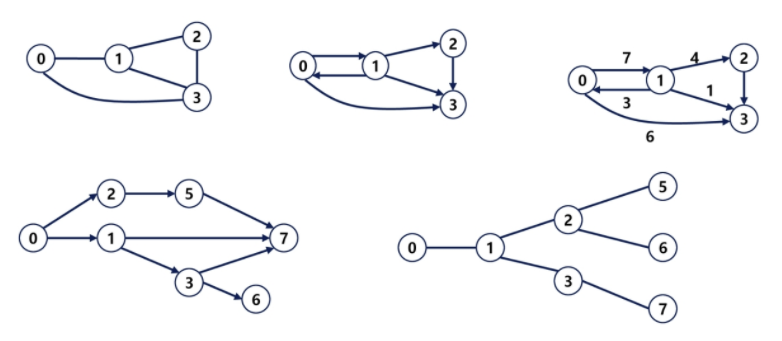 출처 : https://velog.io/@tomato2532/%EA%B7%B8%EB%9E%98%ED%94%84 다양한 그래프의 형태
출처 : https://velog.io/@tomato2532/%EA%B7%B8%EB%9E%98%ED%94%84 다양한 그래프의 형태
그래프 관련 용어
- 노드(node): 위치라는 개념 (그래프에선 정점(vertex)라고도 함)
- 간선(edge): 위치 간의 관계 노드를 연결하는 선 (link, branch 라고도 부름)
- 인접 정점(adjacent vertex): 간선에 의 해 직접 연결된 정점(노드)
- 정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
- 진출 차수(out-degree): 방향 그래프에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
- 경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(simple path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
- 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프의 특징
- 그래프는 객체와 이에 대한 관계를 나타내는 유연한 방식인 네트워크 모델임
- 하나의 노드에 2개 이상의 경로가 가능
- 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있음
- self-loop 뿐 아니라 loop/circuit 모두 가능
- 루트 노드, 부모-자식 관계라는 개념이 없음 (트리는 특수한 형태의 그래프의 일종)
- 순회는 DFS나 BFS로 이루어짐
그래프의 종류
무방향 그래프 vs 방향 그래프
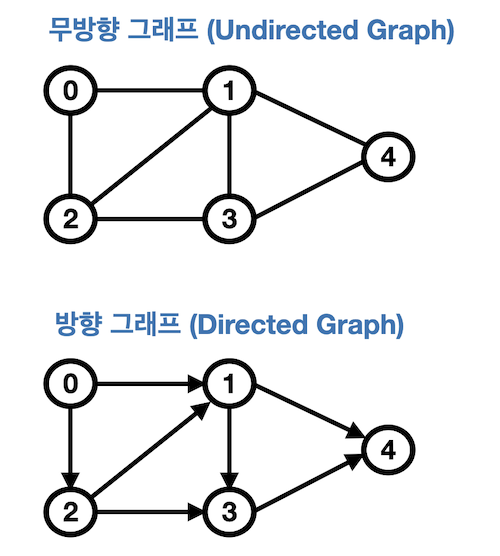 출처 : https://velog.io/@roro/ 무방향 그래프 vs 방향 그래프
출처 : https://velog.io/@roro/ 무방향 그래프 vs 방향 그래프
- 무방향 그래프 (Undirected Graph)
- 무방향 그래프의 노드는 간선을 통해서 양방향으로 갈 수 있음
- 노드가 연결 되어 있을 경우 (A,B) 식으로 표현 ((B,A)와 동일)
- 무방향 그래프에 존재하는 노드의 모든 차수의 합 = 그래프의 간선 수의 2배
- 방향 그래프(Dircted Graph)
- 간선에 방향성이 존재하는 그래프
- 노드가 A -> B로 가는 간선이 연결되어 있을 경우 <A,B> 식으로 표현 (<B,A>와는 상이)
- 방향 그래프에 있는 노드의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수)
연결 그래프 vs 비연결 그래프
 출처 : https://velog.io/@roro/ 연결 그래프 vs 비연결 그래프
출처 : https://velog.io/@roro/ 연결 그래프 vs 비연결 그래프
- 연결 그래프 (Connected Graph)
- 무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우
- 비연결 그래프(Disconnected Graph)
- 무방향 그래프에서 특정 노드에 대해 경로가 존재하지 않는 경우
가중치 그래프
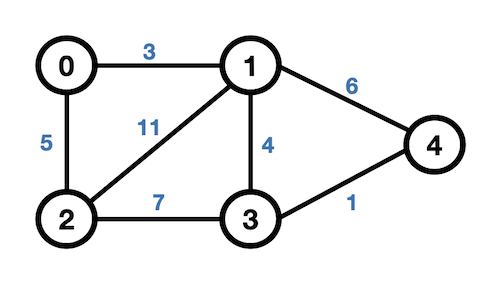 출처 : https://velog.io/@roro/ 가중치 그래프
출처 : https://velog.io/@roro/ 가중치 그래프
- 가중치 그래프 (Weighted Graph)
- 간선에 가중치 또는 비용이 할당된 그래프
- 네트워크 라고도 함 (도시-도시 연결, 통신망의 사용료, 회로 소자의 용량 등)
완전 그래프
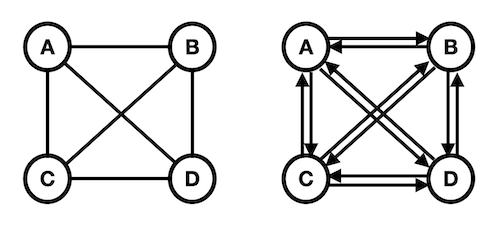 출처 : https://velog.io/@roro/ 완전 그래프
출처 : https://velog.io/@roro/ 완전 그래프
- 완전 그래프 (Complete Graph)
- 그래프의 모든 노드가 서로 연결되어 있는 그래프
- N개의 정점을 가지는 무방향 완전 그래프 -> 간선의 개수 = (N(N-1))/2
- N개의 정점을 가지는 방향 완전 그래프 -> 간선의 개수 = N(N-1)
사이클 vs 비순환 그래프
- 사이클 (Cycle)
- 단순 경로의 시작 노드와 종료 노드가 동일한 경우
- 비순환 그래프(Acyclic Graph)
그래프의 구현
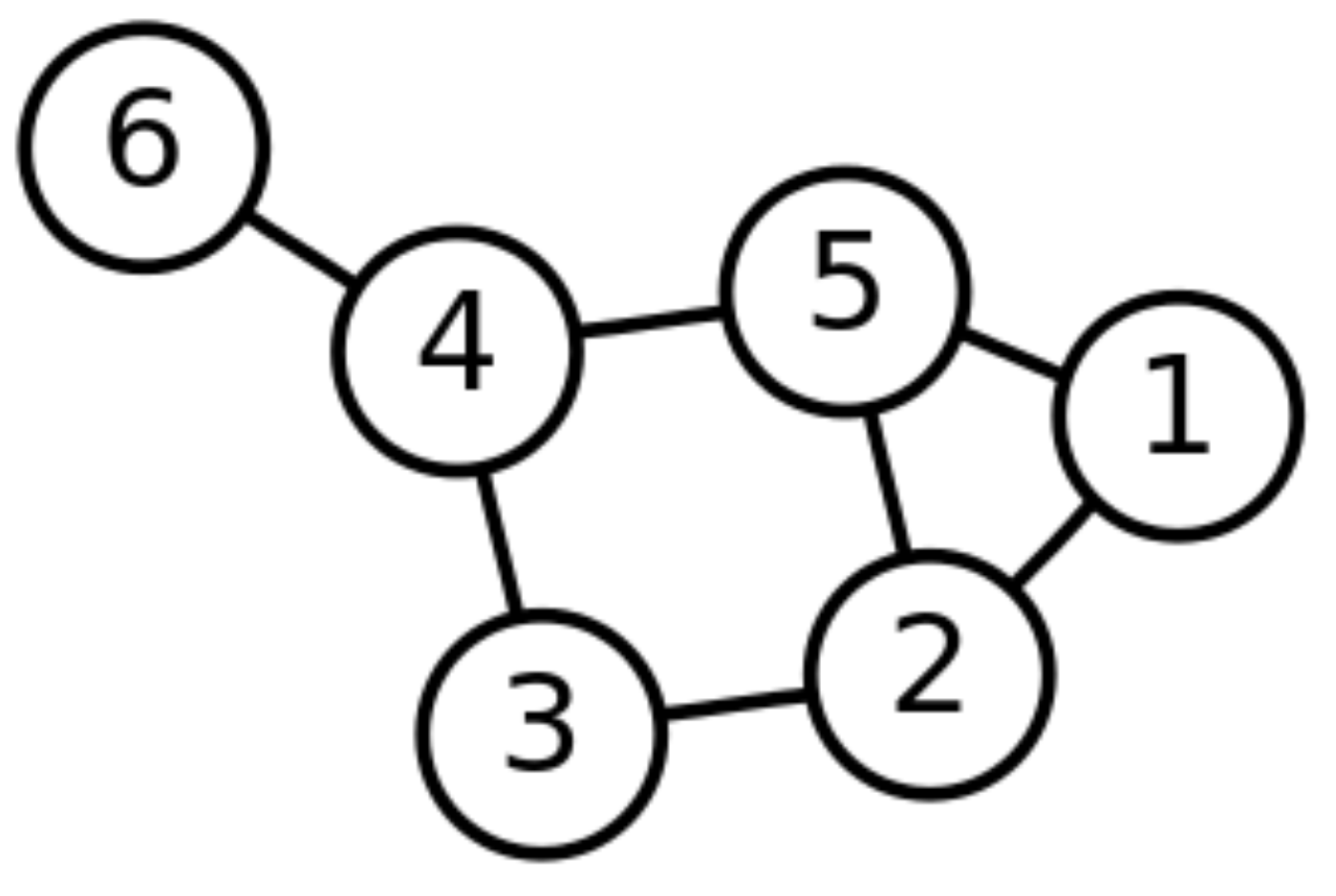
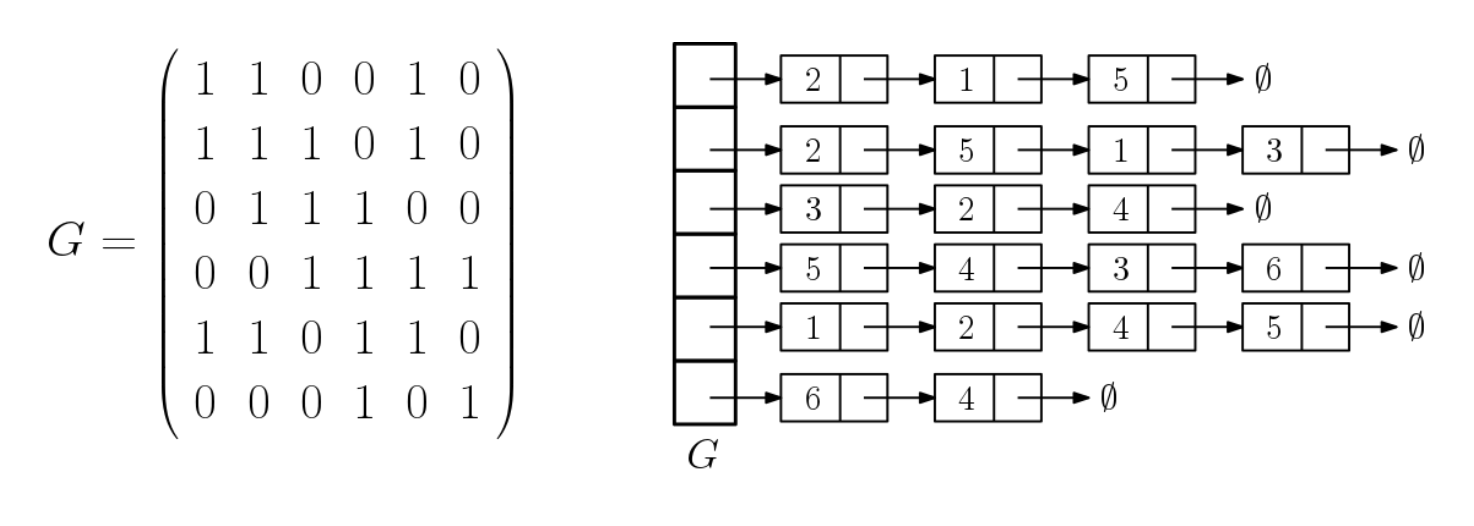 출처 : https://www.youtube.com/user/cssin829 인접 행렬 vs 인접 리스트
출처 : https://www.youtube.com/user/cssin829 인접 행렬 vs 인접 리스트
인접 행렬 (Adjacency Matrix)
- NxN boolin 행렬으로 G[u][v]가 true면 u -> v로의 간선이 있다는 뜻
- 가중치 그래프에서는 boolin값이 아니라 가중치 값이 들어가 있을 수 있음
Continue reading
Heap 힙
- 데이터에서 최대값이나 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리
- 배열에 데이터를 넣고 최대값이나 최소값을 찾으려면 O(n)의 시간이 걸리지만, 힙에서는 O(logn)이 걸림
- 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 등에 활용됨
- 힙에는 부모노드의 키 값이 자식노드의 키 값보다 항상 큰 ‘최대 힙’과 부모노드의 키 값이 자식노드의 키 값보다 항상 작은 ‘최소 힙’ 두가지의 종류가 있음
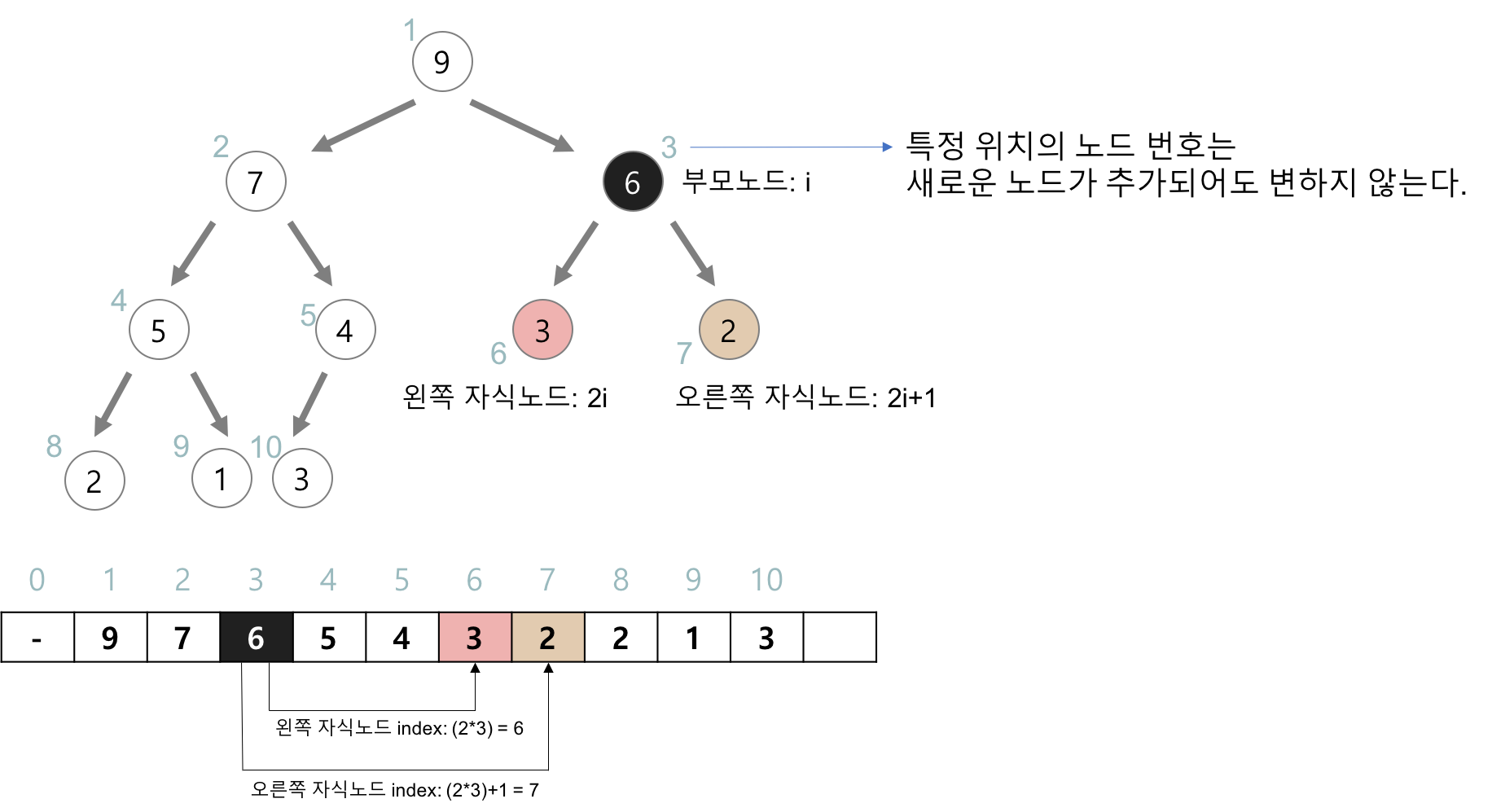 출처 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html 힙의 형태
출처 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html 힙의 형태
- 일반적으로 힙을 저장하는 자료구조로는 배열로 구현
- 구현의 편의성을 위해 배열의 첫번째 인덱스(0)은 None으로 비워 둠
- (부모 노드 인덱스) = (자식 노드 인덱스) // 2
- (왼쪽 자식 노드 인덱스) = (부모 노드 인덱스) * 2
- (오른쪽 자식 노드 인덱스) = (부모 노드 인덱스) * 2 + 1
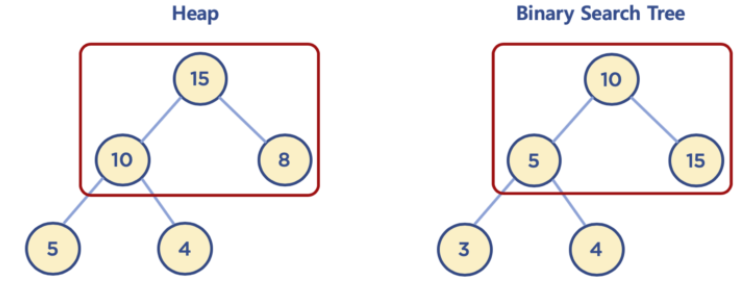 출처 : https://www.fun-coding.org/Chapter11-heap.html 힙과 이진 탐색 트리의 차이점
출처 : https://www.fun-coding.org/Chapter11-heap.html 힙과 이진 탐색 트리의 차이점
- 완전 이진 트리인 힙과 이진 탐색 트리는 여러 차이점이 있음
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음 (최대 힙일 경우 / 최소 힙이면 반대)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고 오른쪽 자식 노드가 가장 크지만, 힙은 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 이진 탐색 트리는 탐색을 위한 구조이고 힙은 최대,최소값 검색을 위한 구조 중 하나
힙 구현
Continue reading
Tree 트리
- 일반적으로 대상 정보의 각 항목들을 계층적으로 연관되도록 구조화시키고자 할 때 사용하는 비선형 자료구조
- Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 한 개의 루트 노드만이 존재하며, 모든 자식 노드는 한 개의 부모 노드만을 가짐 (즉, 루트에서 어떤 노드로 가는 경로는 유일)
- 보통 이진 트리(Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
트리 관련 용어
- 노드 (Node) : 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- 간선 (Branch) : 노드를 연결하는 선 (edge, link라고도 부름)
- 내부 노드 (Internal Node) : 말단 노드가 아닌 노드
- 루트 노드 (Root Node) : 트리 맨 위에 있는 노드
- 말단 노드 (Leaf Node) : 자식 노드가 하나도 없는 노드 (단말 노드, 잎 노드)
- 부모 노드 (Parent Node) : 어떤 노드의 다음 레벨에 연결된 노드
- 자식 노드 (Child Node) : 어떤 노드의 하위 레벨에 연결된 노드
- 형제 노드 (Brother Node) : 동일한 부모 노드를 가진 노드 (Sibling)
- 노드의 레벨 (Level): 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- 노드의 크기 (Size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이 (Depth) : 트리에서 노드가 가질 수 있는 최대 레벨
- 노드의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
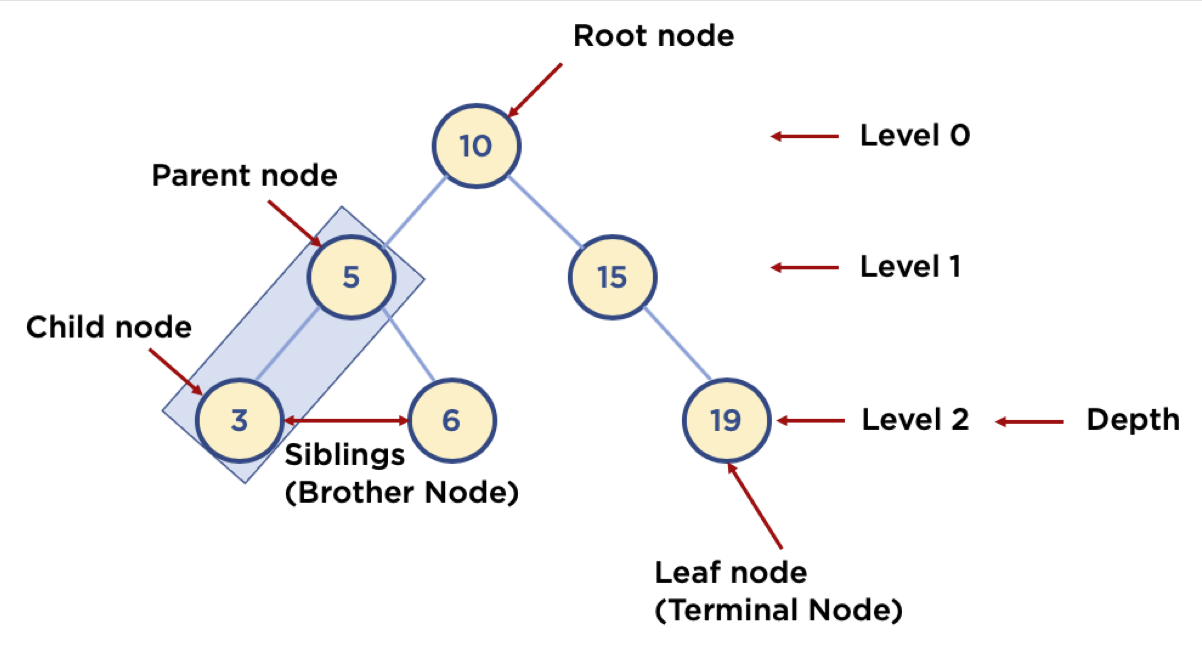 출처 : https://www.fun-coding.org/Chapter10-tree.html 트리 관련 용어 정리
출처 : https://www.fun-coding.org/Chapter10-tree.html 트리 관련 용어 정리 트리의 종류
- 이진 트리 (Binary Tree) : 노드의 최대 Branch가 2인 트리
- 완전 이진 트리 (Complete Binary Tree) : 노드를 삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리
- 전 이진 트리 (Full Binary Tree) : 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
- 포화 이진 트리 (Perfect Binary Tree) : 모든 내부 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는 트리
- 편향 트리 (Skewed Tree) : 한쪽으로 기울어진 트리, 사향 트리라고도 부름
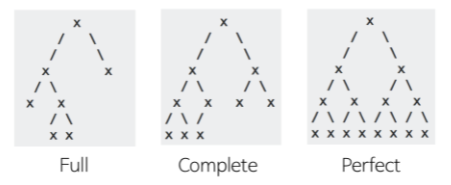 출처 : https://velog.io/@adam2/TREE 이진 트리의 종류
출처 : https://velog.io/@adam2/TREE 이진 트리의 종류
이진 탐색 트리 (Binary Search Tree, BST)
왼쪽 노드는 해당 노드보다 작거나 같은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지는 추가적인 조건이 있는 이진 트리
 출처 : https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node 이진 탐색 트리
출처 : https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node 이진 탐색 트리 Continue reading
날짜: 2021년 6월 29일
소요 시간: 32분 53초
카테고리: 수학문제
태그: 레벨1, 파이썬
Continue reading
날짜: 2021년 6월 25일
소요 시간: 2시간 초과
카테고리: 문자열, 브루트포스 알고리즘, 백트래킹
태그: gold.5, 1342, 파이썬, time out
Continue reading