[leetcode / 206] Reverse Linked List
in Problem Solving on leetcode
날짜: 2021년 8월 25일
카테고리: 연결 리스트
태그: Easy, 206, 파이썬
[leetcode / 21] Merge Two Sorted Lists
in Problem Solving on leetcode
날짜: 2021년 8월 25일
카테고리: 연결 리스트
태그: Easy, 21, 파이썬
[leetcode / 15] 3Sum
in Problem Solving on leetcode
날짜: 2021년 8월 24일
카테고리: 배열
태그: Medium, 15, 파이썬
[leetcode / 42] Trapping Rain Water
in Problem Solving on leetcode
날짜: 2021년 8월 24일
카테고리: 배열
태그: Hard, 42, 파이썬
[leetcode / 1] Two Sum
in Problem Solving on leetcode
날짜: 2021년 8월 24일
카테고리: 배열
태그: Easy, 1, 파이썬
[leetcode / 5] Longest Palindromic Substring
in Problem Solving on leetcode
날짜: 2021년 8월 23일
카테고리: 문자열
태그: Medium, 5, 파이썬
[leetcode / 49] Group Anagrams
in Problem Solving on leetcode
날짜: 2021년 8월 23일
카테고리: 문자열
태그: Medium, 49, 파이썬
[leetcode / 819] Most Common Word
in Problem Solving on leetcode
날짜: 2021년 8월 23일
카테고리: 문자열
태그: Easy, 819, 파이썬
[Algorithm] Minimum Spanning Tree
in Computer Science on Algorithm
Spanning Tree 신장 트리
- 원래의 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 최소 연결 부분 그래프
- n개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개이고, (n-1)개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 됨
- 신장 트리의 조건
- 본래의 그래프의 모든 노드를 포함
- 모든 노드가 서로 연결
- 사이클이 존재하지 않음
Minimum Spanning Tree 최소 신장 트리
[Algorithm] Union-Find Algorithm
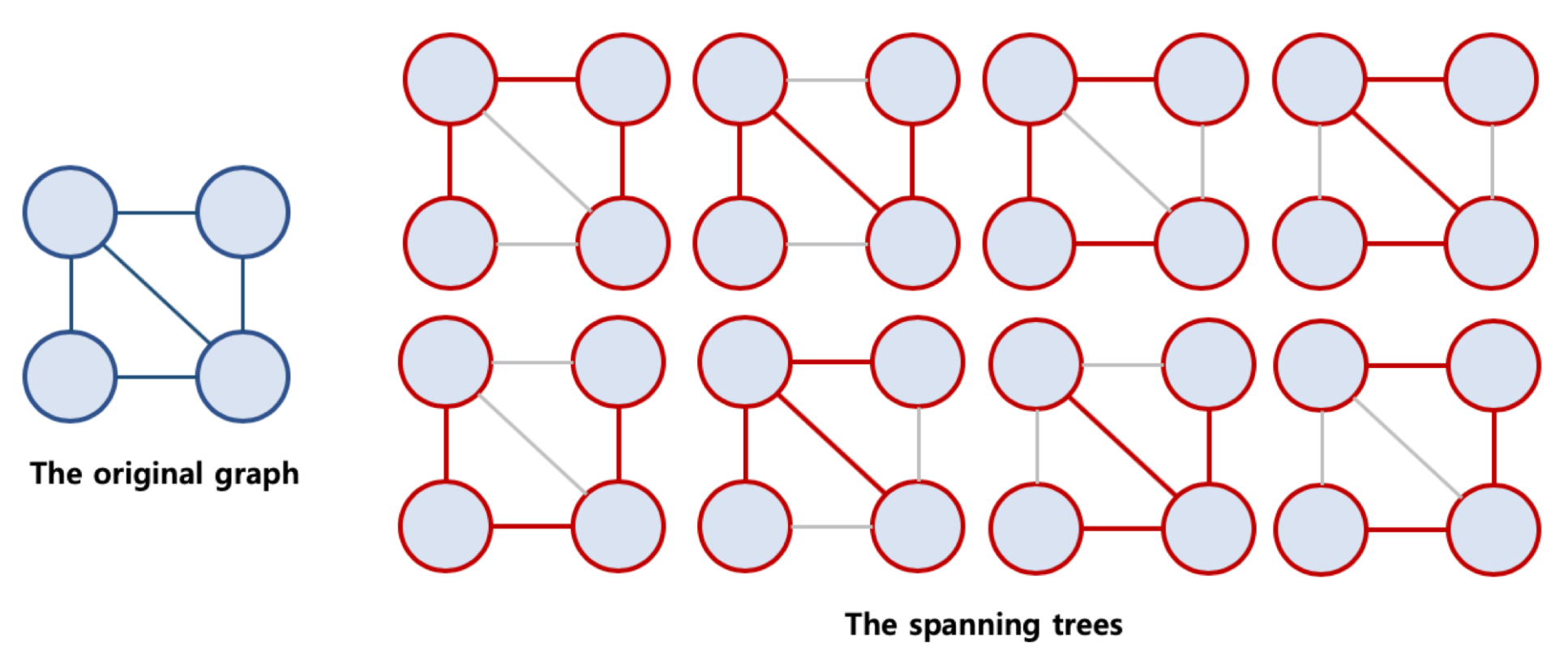
in Computer Science on Algorithm
Union-Find Algorithm 유니온 파인드 알고리즘
- 대표적 그래프 알고리즘으로 합집합 찾기 라는 의미를 가지고 있음
- 주어지는 개체들이 중복된 값을 가지지 않는 별개의 개체들 즉, 집합들간에 교집합이 없는 집합을 상호배타적 집합(Disjoint Set) 또는 서로소 집합이라 할 수 있는데 이런 문제를 풀 때 사용되는 알고리즘으로 주요 연산의 이름에서 따와 Union-find 알고리즘이라 부름
- 여러 노드가 존재할 때 두개의 노드를 선택해서 현재 두 노드가 서로 같은 그래프에 속하는지 판별하고 두개의 노드를 같은 집합으로 묶어주는 알고리즘
- make-set : n 개의 원소가 개별 집합으로 이뤄지도록 초기화
- Union : 두 개별 집합을 하나의 트리로 합치는 연산
- Find : 두 개의 노드를 선택해서 서로 같은 그래프에 속하는지 판별하기 위해 각 그룹의 루트 노드를 확인
Union-Find 알고리즘 로직
- Union 순서에 따라서, 최악의 경우 완전 비대칭 형태의 트리인 링크드 리스트와 같은 형태가 될 수 있음
- Find-Union 시 시간복잡도가 O(n) 이 될 수 있으므로, 해당 문제를 해결하기 위해, union-by-rank, path compression 기법을 사용함
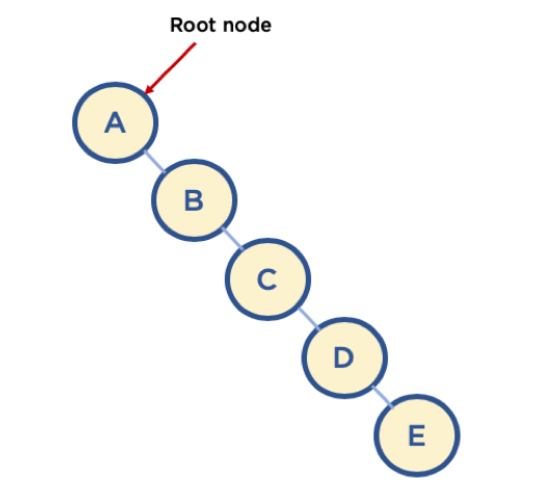
make-set 초기화
