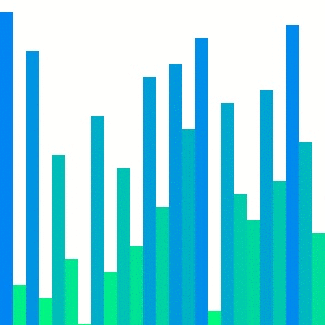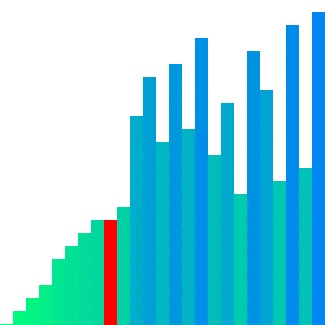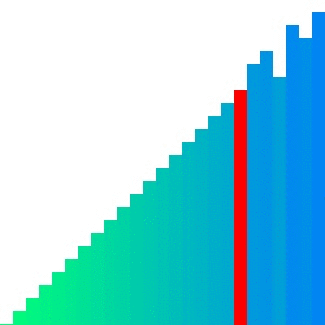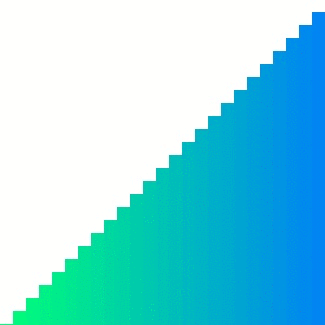Spanning Tree 신장 트리
- 원래의 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 최소 연결 부분 그래프
- n개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개이고, (n-1)개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 됨
- 신장 트리의 조건
- 본래의 그래프의 모든 노드를 포함
- 모든 노드가 서로 연결
- 사이클이 존재하지 않음
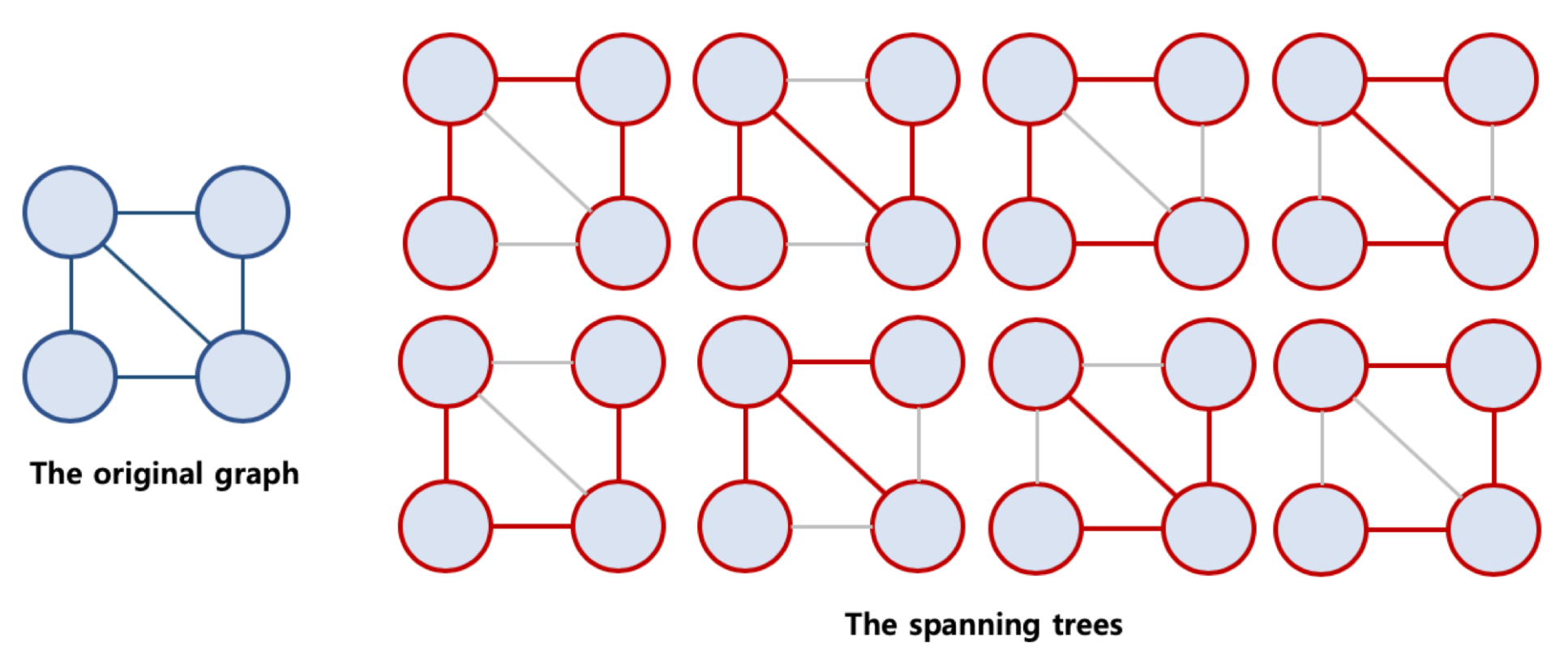 출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 하나의 그래프에서 나올 수 있는 신장트리 형태의 예시
출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 하나의 그래프에서 나올 수 있는 신장트리 형태의 예시
Minimum Spanning Tree 최소 신장 트리
Continue reading
Union-Find Algorithm 유니온 파인드 알고리즘
- 대표적 그래프 알고리즘으로 합집합 찾기 라는 의미를 가지고 있음
- 주어지는 개체들이 중복된 값을 가지지 않는 별개의 개체들 즉, 집합들간에 교집합이 없는 집합을 상호배타적 집합(Disjoint Set) 또는 서로소 집합이라 할 수 있는데 이런 문제를 풀 때 사용되는 알고리즘으로 주요 연산의 이름에서 따와 Union-find 알고리즘이라 부름
- 여러 노드가 존재할 때 두개의 노드를 선택해서 현재 두 노드가 서로 같은 그래프에 속하는지 판별하고 두개의 노드를 같은 집합으로 묶어주는 알고리즘
- make-set : n 개의 원소가 개별 집합으로 이뤄지도록 초기화
- Union : 두 개별 집합을 하나의 트리로 합치는 연산
- Find : 두 개의 노드를 선택해서 서로 같은 그래프에 속하는지 판별하기 위해 각 그룹의 루트 노드를 확인
Union-Find 알고리즘 로직
- Union 순서에 따라서, 최악의 경우 완전 비대칭 형태의 트리인 링크드 리스트와 같은 형태가 될 수 있음
- Find-Union 시 시간복잡도가 O(n) 이 될 수 있으므로, 해당 문제를 해결하기 위해, union-by-rank, path compression 기법을 사용함
 출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 최악의 경우로 Union된 형태
출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 최악의 경우로 Union된 형태
make-set 초기화
 출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 각 원소 초기화 단계
출처 : https://www.fun-coding.org/Chapter20-kruskal-live.html 각 원소 초기화 단계
Continue reading
Backtracking 백트래킹
- 정답을 찾는 도중 정답의 조건에서 벗어난다면 다른 가능성으로 되돌아가서 정답을 찾아가는 기법
- 가능한 모든 방법을 탐색하는 완전 탐색의 일종이지만 가지치기를 통해 비효율적인 경로를 배제하고 탐색하기에 가지치기의 효율에 따라 효율성 극대화
- 트리 구조를 기반으로 DFS로 깊이 탐색을 진행하면서 각 루트에 대해 조건이 부합하는지 확인(Promising)하고 만약 해당 트리에서 조건에 맞지 않는 노드는 더 이상 탐색을 진행하지 않고 가지를 쳐버림(Pruning)
- 주로 재귀 혹은 스택을 통한 DFS로 구현
- 유망성 검토 (Promising) 후 조건에 부합하지 않으면 가지치기(Pruning)를 통해 다른 자손 노드를 탐색함으로서 풀이시간 단축
State Space Tree 상태 공간 트리
- 실제 구현 시 고려할 수 있는 모든 경우의 수를 상태 공간 트리(State Space Tree)를 통해 표현
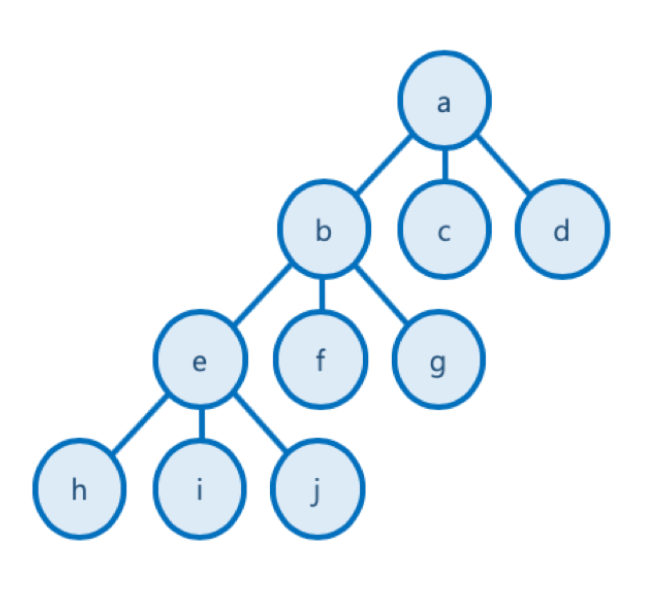 출처 : https://www.fun-coding.org/Chapter21-backtracking-live.html 문제 해결 과정의 중간 상태를 각각의 노드로 나타낸 트리
출처 : https://www.fun-coding.org/Chapter21-backtracking-live.html 문제 해결 과정의 중간 상태를 각각의 노드로 나타낸 트리
N-Queen 문제
- N x N 크기의 체스판에 가로,세로,대각선으로 어느 위치든 이동할 수 있는 퀸을 서로 공격할 수 없는 위치로 최대한 많이 배치하는 대표적인 백트래킹 문제
N-Queen 문제 해결 로직
- 퀸은 수평 이동이 가능하므로 한 행에는 하나의 퀸 밖에 위치할 수 없음
- 맨 위에 있는 행부터 퀸을 배치하고, 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치
- 만약 앞선 행에 배치한 퀸으로 인해, 다음 행에 해당 퀸들이 이동할 수 없는 위치가 없을 경우에는, 더 이상 퀸을 배치하지 않고, 이전 행의 퀸의 배치를 바꿈
- 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후, 각 경우를 맨 위의 행부터 DFS 방식으로 접근
- 해당 경우가 진행이 어려울 경우, 더 이상 진행하지 않고, 다른 경우를 체크
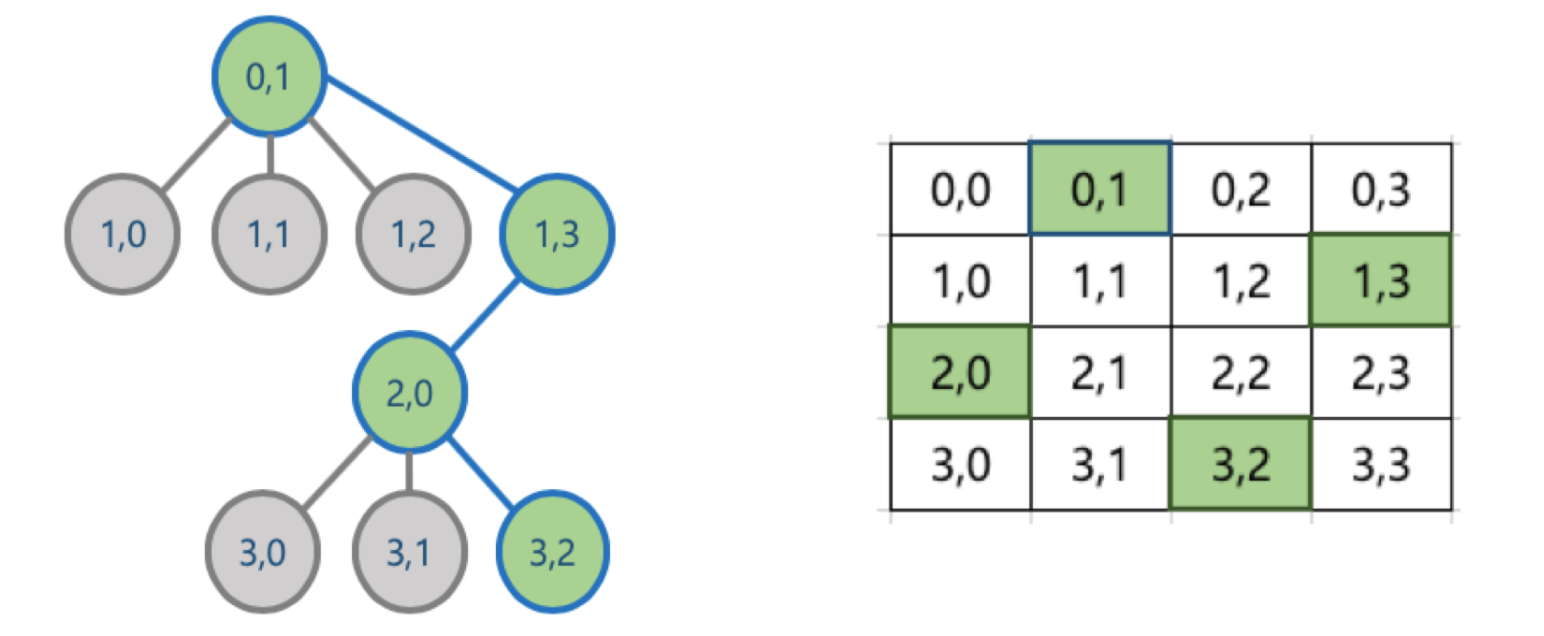 출처 : https://www.fun-coding.org/Chapter21-backtracking-live.html 4-Queen 문제 상태 공간 트리
출처 : https://www.fun-coding.org/Chapter21-backtracking-live.html 4-Queen 문제 상태 공간 트리
N-Queen 문제 알고리즘 구현
```python def is_available(candidate, current_col): current_row = len(candidate) for queen_row in range(current_row):
if candidate[queen_row] == current_col or abs(candidate[queen_row] - current_col) == current_row - queen_row: return False return True
Continue reading
Shortest Path Problem 최단 경로 문제
- 최단 경로 문제란 두 노드를 잇는 가장 짧은 경로를 찾는 문제
- 가중치 그래프 (Weighted Graph) 에서 간선 (Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적
최단 경로 문제 종류
- 단일 출발 및 단일 도착 (single-source and single-destination shortest path problem) 최단 경로 문제
- 그래프 내의 특정 노드 u 에서 출발, 또다른 특정 노드 v 에 도착하는 가장 짧은 경로를 찾는 문제
- 단일 출발 (single-source shortest path problem) 최단 경로 문제
- 그래프 내의 특정 노드 u 와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제
- 전체 쌍(all-pair) 최단 경로 문제
- 그래프 내의 모든 노드 쌍 (u, v) 에 대한 최단 경로를 찾는 문제
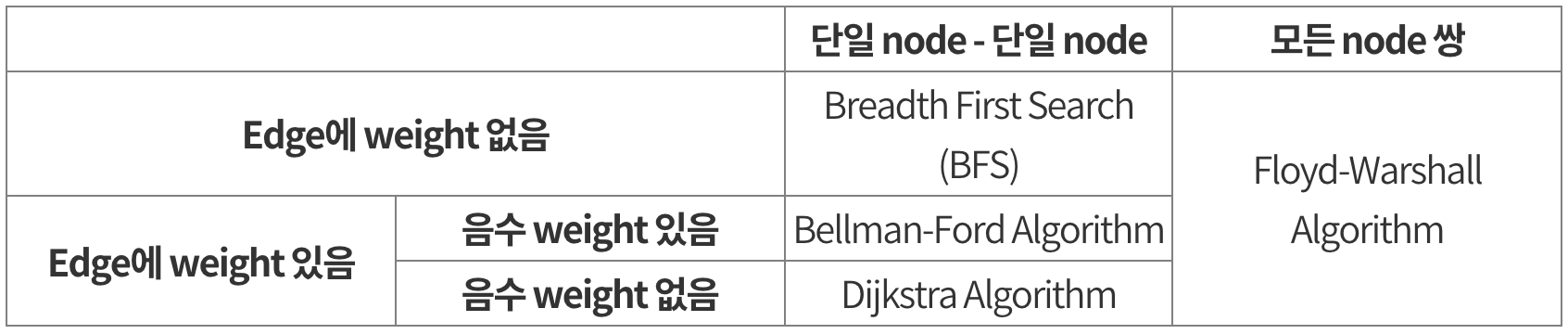 출처 : https://shnoh.tistory.com/15 상황에 따라 사용해야 할 최단 경로 문제 알고리즘
출처 : https://shnoh.tistory.com/15 상황에 따라 사용해야 할 최단 경로 문제 알고리즘
Dijkstra Algorithm 다익스트라 알고리즘
- 하나의 노드에서 다른 모든 노드 간의 각각 가장 짧은 거리를 구하는 단일 출발 최단 경로 문제에 적합
- 첫 노드을 기준으로 연결되어 있는 노드들을 추가해 가며, 최단 거리를 갱신하는 기법으로 BFS와 유사
다익스트라 알고리즘 로직
- 다익스트라 알고리즘의 다양한 변형 로직이 있지만, 본 포스팅에서는 가장 개선된 우선순위 큐를 사용하는 방식을 사용
- 우선순위 큐는 최소 힙 방식을 활용해서, 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼냄
- 첫 노드를 기준으로 배열을 선언하여 첫 노드에서 각 노드까지의 거리를 저장
- 시간을 단축시키기 위해 접근이 빠른 해시테이블의 성질을 띄는 딕셔너리로 선언
- 초기에는 첫 노드의 거리는 0, 나머지는 무한대(inf)로 저장
- 우선순위 큐에 (첫 노드, 거리 0)만 먼저 넣음
- 우선순위 큐에서 노드를 꺼냄
- 처음에는 첫 노드만 저장되어 있으므로, 첫 노드가 꺼내짐
- 첫 노드에 인접한 노드들 각각에 대해, 첫 노드에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 노드에서 각 노드까지의 거리를 비교
- 배열에 저장되어 있는 거리보다, 첫 노드에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리로 업데이트
- 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 삽입
- 결과적으로 너비 우선 탐색 방식과 유사하게, 첫 노드에 인접한 노드들을 순차적으로 방문
- 만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드, 거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않음
- 2번의 과정을 우선순위 큐에 꺼낼 노드가 없을 때까지 반복
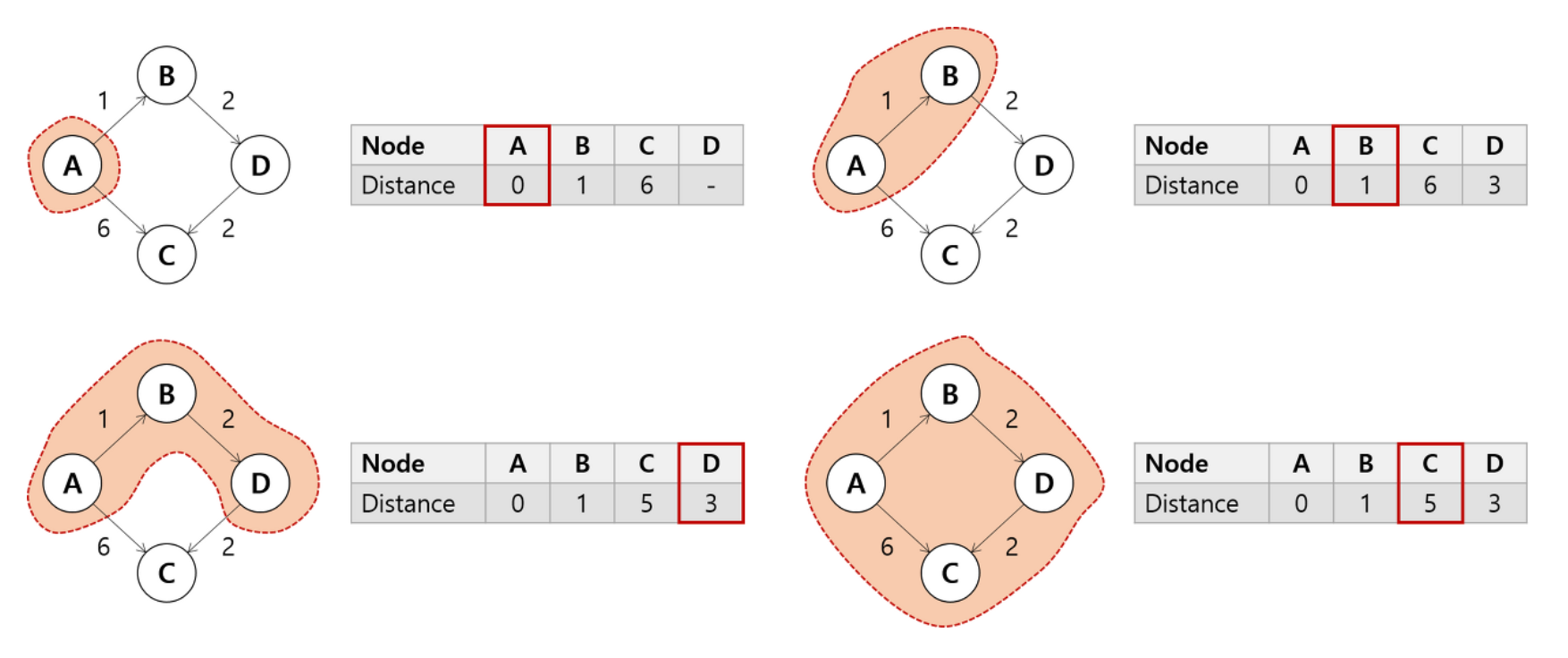 출처 : https://shnoh.tistory.com/15 우선순위 큐 방식의 다익스트라 알고리즘 로직
출처 : https://shnoh.tistory.com/15 우선순위 큐 방식의 다익스트라 알고리즘 로직
다익스트라 알고리즘 구현
Continue reading
BFS (Breadth First Search) 너비 우선 탐색
- 정점들과 같은 레벨에 있는 노드들(형제 노드들)을 먼저 탐색하는 방식
- 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함
- 주로 queue를 활용하여 구현함
Continue reading
Search Algorithm 탐색 알고리즘
- 탐색은 여러 데이터 중 원하는 데이터를 찾아내는 것을 의미함
- 검색 엔진에 탐색 알고리즘이 많이 사용되기도 함 (그래서 검색 알고리즘이라고도 함)
Sequential Search Algorithm 순차 탐색 알고리즘
- 리스트의 가장 처음부터 시작하여 찾으려는 데이터가 나올 때까지 하나씩 리스트의 각 요소와 비교하는 탐색 알고리즘
- Linear Search Algorithm (선형 탐색 알고리즘)이라고 하기도 함
- O(n)의 시간 복잡도를 가짐
def sequencial_Search(data_list, search_data):
for index in range(len(data_list)):
if data_list[index] == search_data:
return True
return False
Binary Search Algorithm 이진 탐색 알고리즘
- 찾으려는 데이터가 나올 때까지 탐색할 리스트를 둘로 나누어가며 탐색 하는 알고리즘
- 이진 탐색은 반드시 리스트가 정렬되어 있는 상태에서 탐색을 진행
- O(nlogn)의 시간 복잡도를 가짐
Continue reading
Greedy Algorithm 탐욕 알고리즘
- 매 순간 최적이라고 생각되는 해를 구해나가는 알고리즘
- 순간순간 최적이라고 생각되는 해를 구해나가기 때문에 보다 빠르게 최적에 가까운 값을 구하기 위해 사용되지만, 그 해가 무조건 최적이 아닐 수도 있기 때문에 상황에 맞게 잘 활용 해야 함
- (특정한 상황일 경우 그리디 알고리즘도 최적의 해를 보장해 줄 수도 있음)
- 대표적으로 그리디 알고리즘을 응용한 알고리즘으로는 다익스트라 알고리즘, 허프만 코드, 크러스컬 알고리즘 등이 있음
대표적인 그리디 알고리즘을 활용한 문제
가장 적은 동전의 수
- 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식으로 구현
```python coin_list = [500, 100, 50, 1]
Continue reading
Dynamic Programing 동적 계획법
- 특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법
- Dynamic이라는 이름과는 다르게 전혀 동적이진 않은데
이는 처음 이 방식을 사용한 벨만이 다른 이유 없이 Dynamic 이라는 단어가 그저 멋있어서 선택했다고 함 - 분할 정복과는 다르게 동적 계획법은 두가지 전제 조건이 있어야 동적 계획법으로 문제를 해결 가능
- Overlapping Subproblem : 겹치는 작은 문제
- 어떤 문제가 여러개의 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀를 통해 해결되는 부분 문제로 쪼개질 수 있을 때
- Optimal Substructure : 최적 부분구조
- 어떤 문제의 최적의 해결책이 그 부분 문제의 최적의 해결책으로 부터 설계될 수 있을 때, 즉, 최적 부분구조 일때 문제의 정답을 작은 문제의 정답에서 부터 구할 수 있음
- 이 속성은 동적 계획법이나 그리디 알고리즘의 유용성을 판별하는데 사용되기도 함
Memoization 메모이제이션
- 동일한 문제를 반복해야 할 경우, 한 번 계산된 결과를 저장해 두었다가 활용하는 방식으로 중복 계산을 줄이는 것
- 동적 계획법을 분할 정복과 나누는 가장 큰 차이점 중 하나
 출처 : https://coding-all.tistory.com/2 중복 제거 전(왼쪽)과 후(오른쪽) 시간복잡도 변화
출처 : https://coding-all.tistory.com/2 중복 제거 전(왼쪽)과 후(오른쪽) 시간복잡도 변화
Continue reading
Divide and conquer 분할 정복
- 분할정복법은 주어진 문제를 작은 사례로 나누고 각각의 작은 문제들을 해결하여 정복 (Conquer)하는 방법
- 분할 정복 패러다임을 차용한 알고리즘들은 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산, 각 부분 문제의 답으로부터 전체 문제의 답을 계산
- 주로 재귀함수를 이용하여 구현하는 것이 일반적이나, 재귀호출을 사용하지 않고 스택, 큐 등의 자료구조를 이용하여 구현하기도 함
- 대표적인 분할 정복법을 활용한 알고리즘으로는 퀵 정렬과 병합 정렬이 있음
분할 정복 프로세스
- Divide (분할) : 문제를 동일한 유형의 여러 하위 문제로 분할
- Conquer (정복) : 가장 작은 단위의 하위 문제들을 해결하며 정복
- Combine (조합) : 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합
문제를 제대로 분할하면 정복하는 것은 쉽기 때문에 제대로 분할하는 것이 중요
분할 정복법은 재귀 호출이 자주 사용되는데, 이 부분에서 분할 정복법의 효율성이 떨어질 수도 있음
분할 정복의 장단점
장점
- 문제를 나누어 해결함으로써 어려운 문제를 보다 쉽게 해결할 수 있음
- 문제를 나누어 해결한다는 특징상 병렬적으로 문제를 해결하는 데 큰 강점이 있음
단점
- 함수를 재귀적으로 호출하게 되면 함수 호출로 인한 오버헤드가 발생하며, 스택에 다양한 데이터를 보관하고 있어야 하므로 스택 오버플로우가 발생하거나 과도한 메모리 사용을 하게 됨
분할 정복 vs 재귀 호출
- 일반적인 재귀 호출과의 차이점은 항상 문제를 한 조각과 나머지로 쪼개는 방식인 재귀 호출과는 달리 분할정복법은 항상 문제를 절반씩으로 나누어 문제를 해결
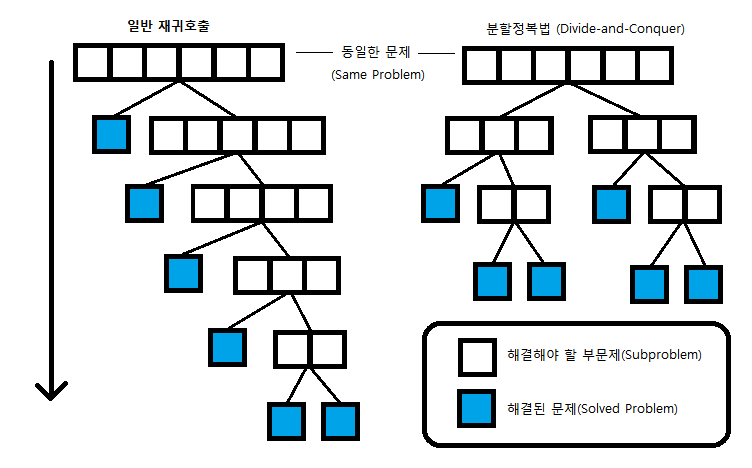 출처 : https://data-make.tistory.com/232 일반적인 재귀와 분할 정복의 차이
출처 : https://data-make.tistory.com/232 일반적인 재귀와 분할 정복의 차이
Continue reading
Recursion 재귀
- 정의 단계에서 자신을 재참조 하는 함수
- 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식
- 재귀 호출이나 되부름 이라고도 함
Continue reading
Sort Algorithm 정렬 알고리즘
Quick Sort 퀵 정렬
- 기준점(pivot)을 정해서 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right)로 모으는 방식
- 평균적으로 매우 빠른 수행 속도를 내는 정렬 방식
- 분할 정복 알고리즘의 하나로, 재귀 알고리즘을 이용한 정렬 방식
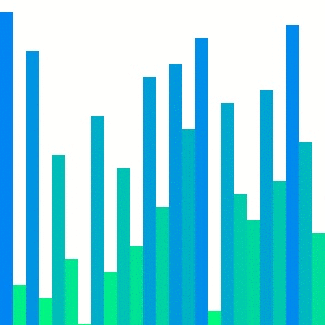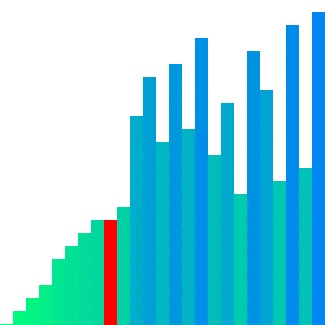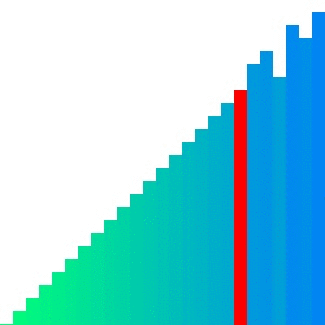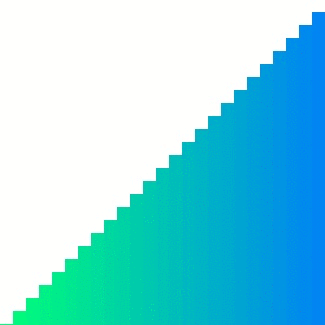 출처 : https://d2.naver.com/helloworld/0315536 퀵 정렬 동작 모습
출처 : https://d2.naver.com/helloworld/0315536 퀵 정렬 동작 모습
동작 원리
- n개의 데이터가 있는 리스트의 첫 번째 데이터를 피벗으로 설정
- 피벗을 기준으로 작은 값과 큰 값을 분류
- 만약 데이터가 피벗보다 작다면
left 리스트에 데이터 추가 - 만약 데이터가 피벗보다 크다면
right 리스트에 데이터 추가
- 리스트의 길이가 1 이하가 될 때 까지
left 리스트와 right 리스트 함수 재귀
```python def quick_sort(data): if len(data) <= 1: return data
Continue reading
Sort Algorithm 정렬 알고리즘
- 어떤 데이터들을 정해진 순서대로 나열하는 것
- 정렬의 목표 : 비교 횟수와 교환 횟수를 최소화
정렬 알고리즘의 성질
- stable sort 안정 정렬 vs unstable sort 불안정 정렬
- 중복된 수의 순서가 유지되는지 안되는지 여부
- Stable Sorting
Bubble Sort 버블 정렬
Insertion Sort 삽입 정렬
Merge Sort 합병 정렬
- Unstable Sorting
Selection Sort 선택 정렬
Heap Sort 힙 정렬
Quick Sort 퀵 정렬
- in-place 제자리 정렬
- 추가적인 메모리 공간을 많이 필요로 하지 않는 혹은 전혀 필요하지 않는 알고리즘을 의미
- 통상적으로, 공간은 O(logn)이고 O(n)이 될 때도 있음
Selection Sort 버블 정렬
Selection Sort 선택 정렬
Insertion Sort 삽입 정렬
Heap Sort 힙 정렬
Quick Sort 퀵 정렬
Bubble Sort 버블 정렬
- 서로 인접한 두 원소를 비교하여 큰 수를 오른쪽으로 하나씩 밀어내어 최댓값을 가장 마지막으로 보내는 정렬
 출처 : https://blog.csdn.net/weixin_42022175/article/details/101203937 버블 정렬 동작 모습
출처 : https://blog.csdn.net/weixin_42022175/article/details/101203937 버블 정렬 동작 모습
Continue reading