Graph 그래프
- 노드와 간선으로 이루어진 노드간의 관계를 표현하는 자료구조
- G = (v,e)로 표현 (v = vertex set / e = edge set)
- 연결되어 있는 객체 간의 조직도를 표현할 수 있는 자료구조
- 지하철 노선도, 도심의 도로 등 실생활에서 다양한 예를 표현 가능
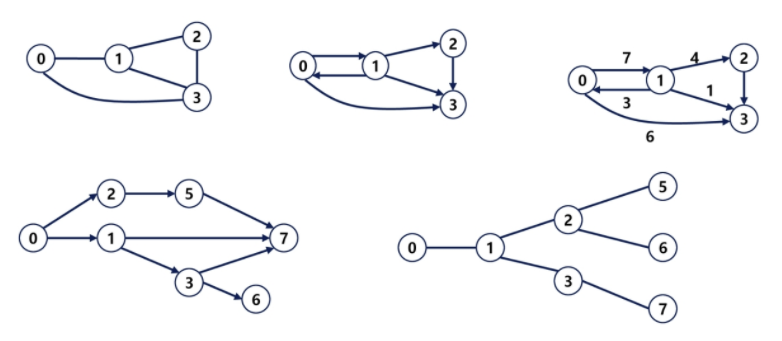 출처 : https://velog.io/@tomato2532/%EA%B7%B8%EB%9E%98%ED%94%84 다양한 그래프의 형태
출처 : https://velog.io/@tomato2532/%EA%B7%B8%EB%9E%98%ED%94%84 다양한 그래프의 형태
그래프 관련 용어
- 노드(node): 위치라는 개념 (그래프에선 정점(vertex)라고도 함)
- 간선(edge): 위치 간의 관계 노드를 연결하는 선 (link, branch 라고도 부름)
- 인접 정점(adjacent vertex): 간선에 의 해 직접 연결된 정점(노드)
- 정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
- 진출 차수(out-degree): 방향 그래프에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
- 경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(simple path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
- 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프의 특징
- 그래프는 객체와 이에 대한 관계를 나타내는 유연한 방식인 네트워크 모델임
- 하나의 노드에 2개 이상의 경로가 가능
- 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있음
- self-loop 뿐 아니라 loop/circuit 모두 가능
- 루트 노드, 부모-자식 관계라는 개념이 없음 (트리는 특수한 형태의 그래프의 일종)
- 순회는 DFS나 BFS로 이루어짐
그래프의 종류
무방향 그래프 vs 방향 그래프
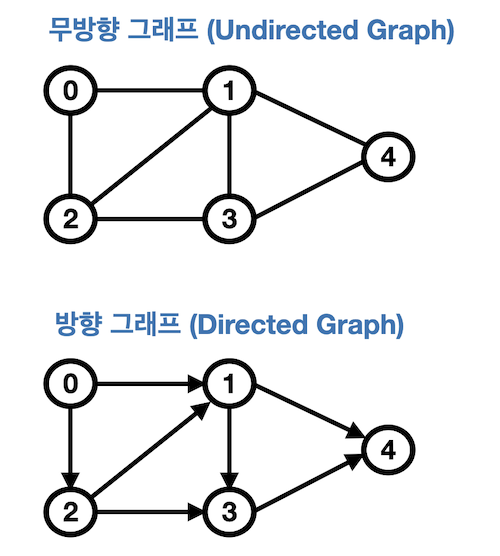 출처 : https://velog.io/@roro/ 무방향 그래프 vs 방향 그래프
출처 : https://velog.io/@roro/ 무방향 그래프 vs 방향 그래프
- 무방향 그래프 (Undirected Graph)
- 무방향 그래프의 노드는 간선을 통해서 양방향으로 갈 수 있음
- 노드가 연결 되어 있을 경우 (A,B) 식으로 표현 ((B,A)와 동일)
- 무방향 그래프에 존재하는 노드의 모든 차수의 합 = 그래프의 간선 수의 2배
- 방향 그래프(Dircted Graph)
- 간선에 방향성이 존재하는 그래프
- 노드가 A -> B로 가는 간선이 연결되어 있을 경우 <A,B> 식으로 표현 (<B,A>와는 상이)
- 방향 그래프에 있는 노드의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수)
연결 그래프 vs 비연결 그래프
 출처 : https://velog.io/@roro/ 연결 그래프 vs 비연결 그래프
출처 : https://velog.io/@roro/ 연결 그래프 vs 비연결 그래프
- 연결 그래프 (Connected Graph)
- 무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우
- 비연결 그래프(Disconnected Graph)
- 무방향 그래프에서 특정 노드에 대해 경로가 존재하지 않는 경우
가중치 그래프
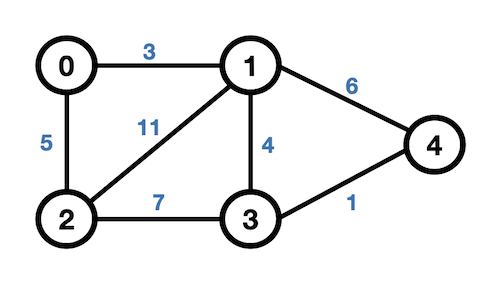 출처 : https://velog.io/@roro/ 가중치 그래프
출처 : https://velog.io/@roro/ 가중치 그래프
- 가중치 그래프 (Weighted Graph)
- 간선에 가중치 또는 비용이 할당된 그래프
- 네트워크 라고도 함 (도시-도시 연결, 통신망의 사용료, 회로 소자의 용량 등)
완전 그래프
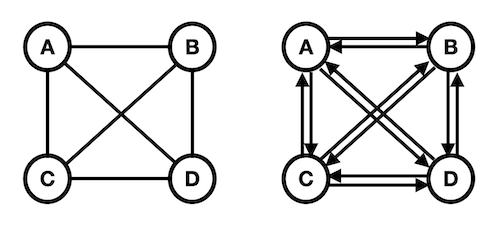 출처 : https://velog.io/@roro/ 완전 그래프
출처 : https://velog.io/@roro/ 완전 그래프
- 완전 그래프 (Complete Graph)
- 그래프의 모든 노드가 서로 연결되어 있는 그래프
- N개의 정점을 가지는 무방향 완전 그래프 -> 간선의 개수 = (N(N-1))/2
- N개의 정점을 가지는 방향 완전 그래프 -> 간선의 개수 = N(N-1)
사이클 vs 비순환 그래프
- 사이클 (Cycle)
- 단순 경로의 시작 노드와 종료 노드가 동일한 경우
- 비순환 그래프(Acyclic Graph)
그래프의 구현
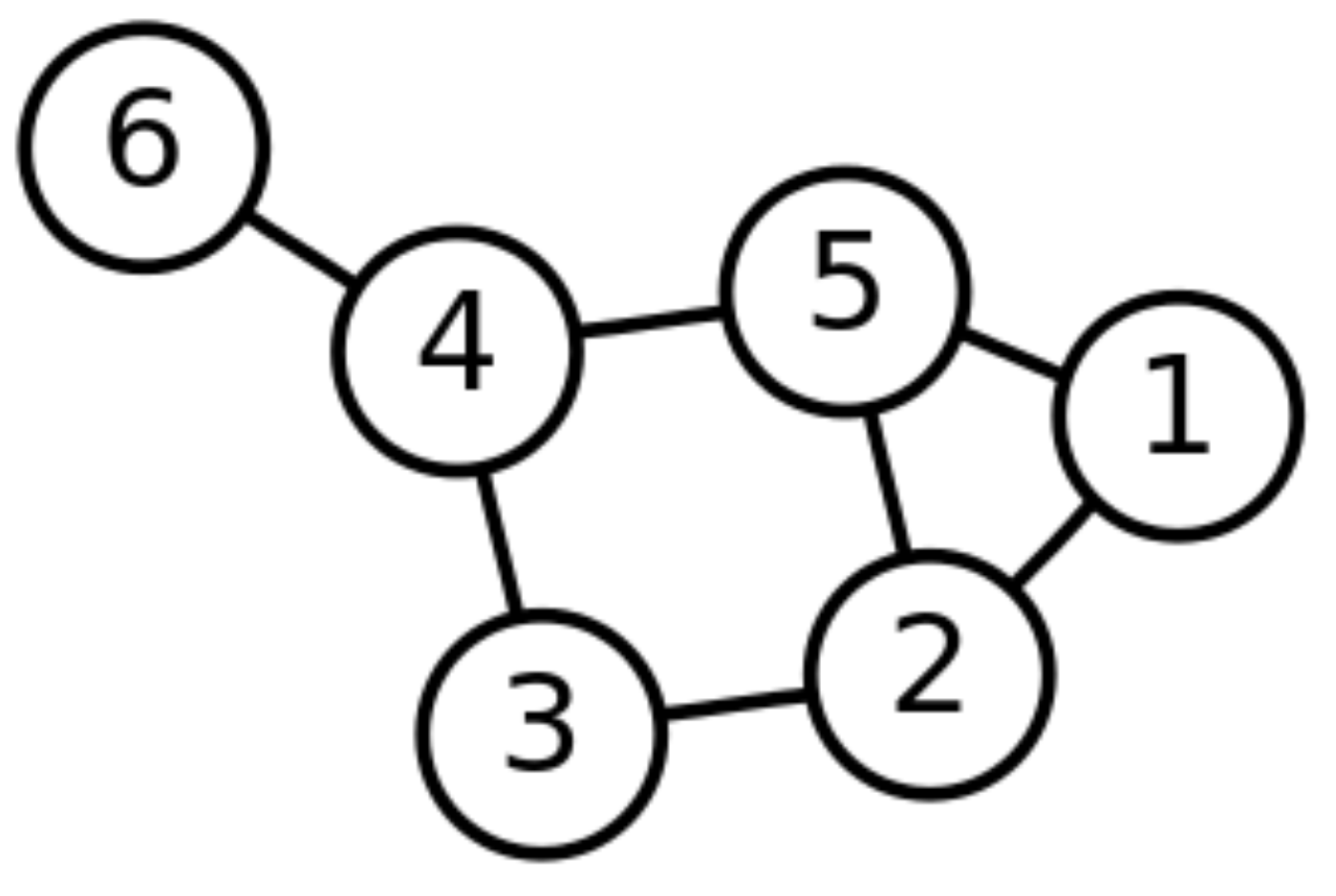
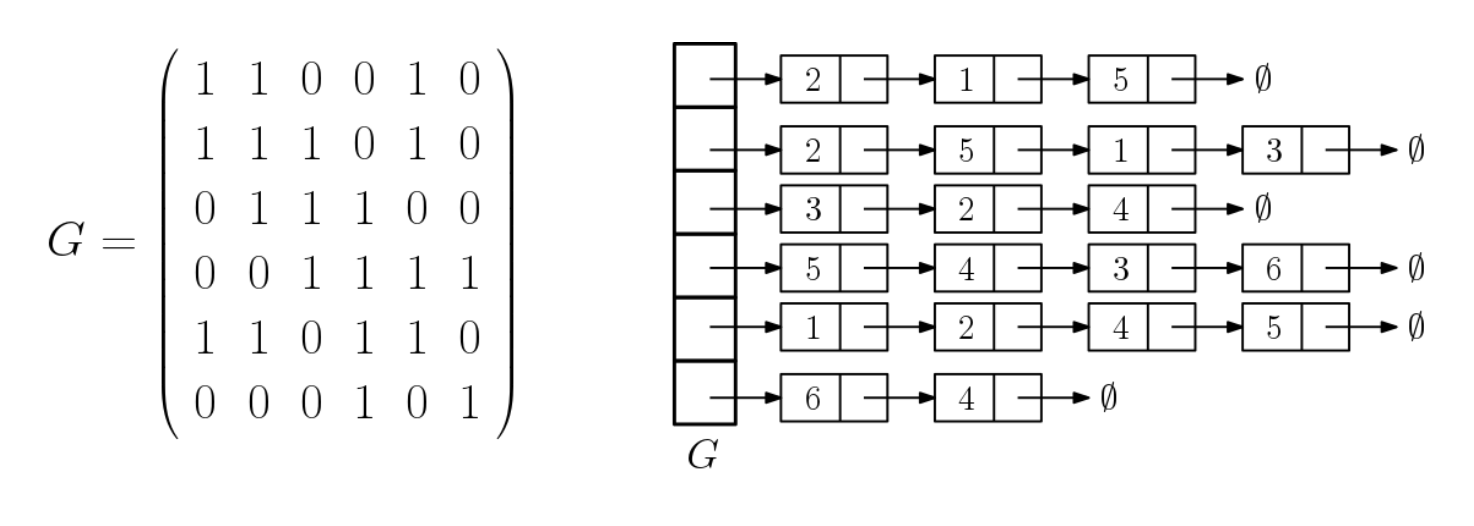 출처 : https://www.youtube.com/user/cssin829 인접 행렬 vs 인접 리스트
출처 : https://www.youtube.com/user/cssin829 인접 행렬 vs 인접 리스트
인접 행렬 (Adjacency Matrix)
- NxN boolin 행렬으로 G[u][v]가 true면 u -> v로의 간선이 있다는 뜻
- 가중치 그래프에서는 boolin값이 아니라 가중치 값이 들어가 있을 수 있음
Continue reading
Heap 힙
- 데이터에서 최대값이나 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리
- 배열에 데이터를 넣고 최대값이나 최소값을 찾으려면 O(n)의 시간이 걸리지만, 힙에서는 O(logn)이 걸림
- 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 등에 활용됨
- 힙에는 부모노드의 키 값이 자식노드의 키 값보다 항상 큰 ‘최대 힙’과 부모노드의 키 값이 자식노드의 키 값보다 항상 작은 ‘최소 힙’ 두가지의 종류가 있음
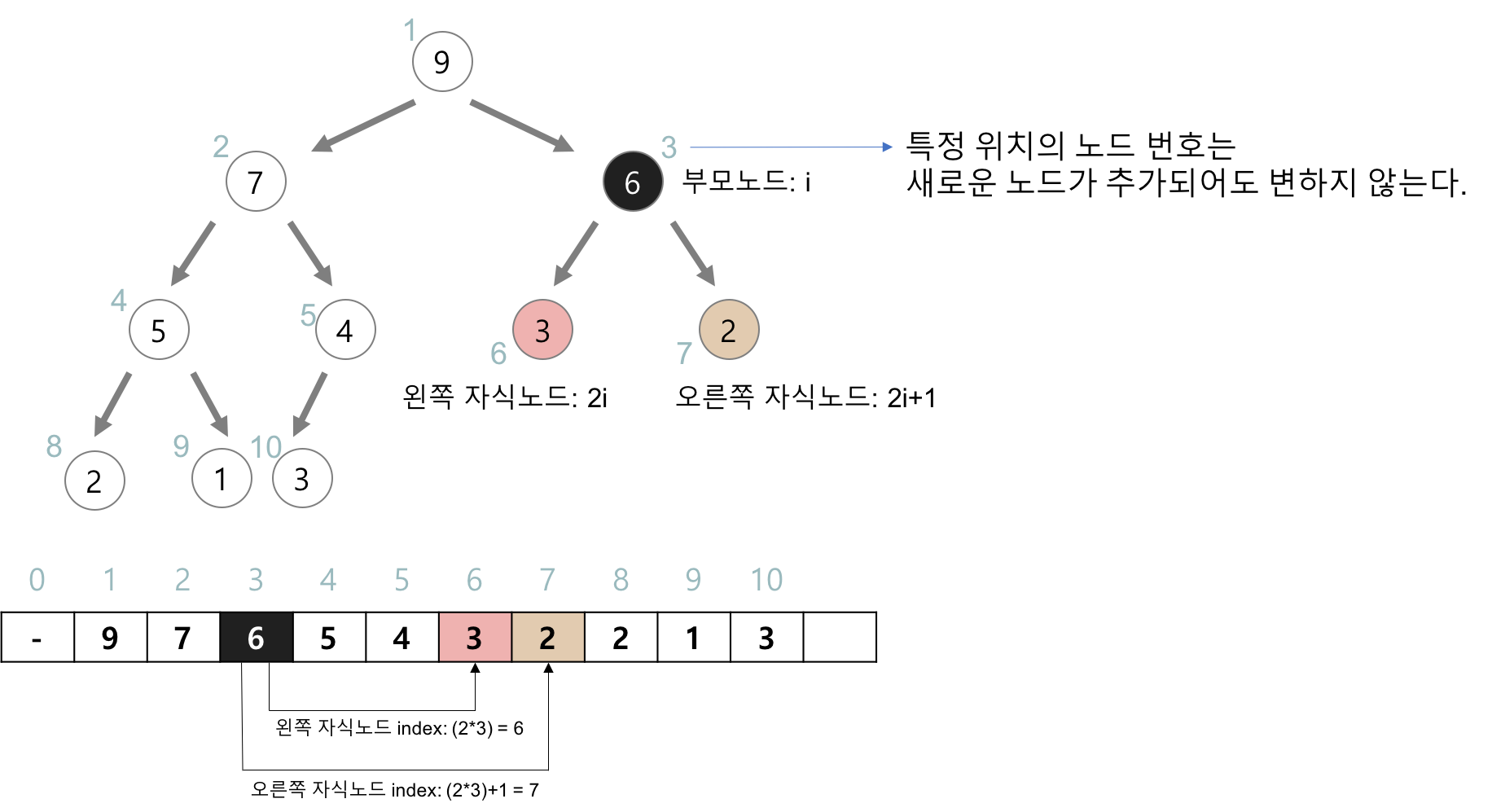 출처 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html 힙의 형태
출처 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html 힙의 형태
- 일반적으로 힙을 저장하는 자료구조로는 배열로 구현
- 구현의 편의성을 위해 배열의 첫번째 인덱스(0)은 None으로 비워 둠
- (부모 노드 인덱스) = (자식 노드 인덱스) // 2
- (왼쪽 자식 노드 인덱스) = (부모 노드 인덱스) * 2
- (오른쪽 자식 노드 인덱스) = (부모 노드 인덱스) * 2 + 1
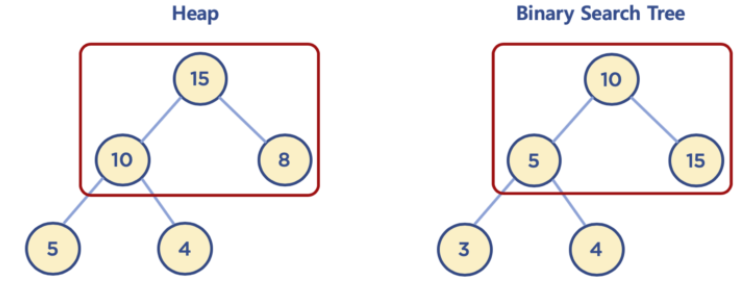 출처 : https://www.fun-coding.org/Chapter11-heap.html 힙과 이진 탐색 트리의 차이점
출처 : https://www.fun-coding.org/Chapter11-heap.html 힙과 이진 탐색 트리의 차이점
- 완전 이진 트리인 힙과 이진 탐색 트리는 여러 차이점이 있음
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음 (최대 힙일 경우 / 최소 힙이면 반대)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고 오른쪽 자식 노드가 가장 크지만, 힙은 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 이진 탐색 트리는 탐색을 위한 구조이고 힙은 최대,최소값 검색을 위한 구조 중 하나
힙 구현
Continue reading
Tree 트리
- 일반적으로 대상 정보의 각 항목들을 계층적으로 연관되도록 구조화시키고자 할 때 사용하는 비선형 자료구조
- Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 한 개의 루트 노드만이 존재하며, 모든 자식 노드는 한 개의 부모 노드만을 가짐 (즉, 루트에서 어떤 노드로 가는 경로는 유일)
- 보통 이진 트리(Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
트리 관련 용어
- 노드 (Node) : 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- 간선 (Branch) : 노드를 연결하는 선 (edge, link라고도 부름)
- 내부 노드 (Internal Node) : 말단 노드가 아닌 노드
- 루트 노드 (Root Node) : 트리 맨 위에 있는 노드
- 말단 노드 (Leaf Node) : 자식 노드가 하나도 없는 노드 (단말 노드, 잎 노드)
- 부모 노드 (Parent Node) : 어떤 노드의 다음 레벨에 연결된 노드
- 자식 노드 (Child Node) : 어떤 노드의 하위 레벨에 연결된 노드
- 형제 노드 (Brother Node) : 동일한 부모 노드를 가진 노드 (Sibling)
- 노드의 레벨 (Level): 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- 노드의 크기 (Size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이 (Depth) : 트리에서 노드가 가질 수 있는 최대 레벨
- 노드의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
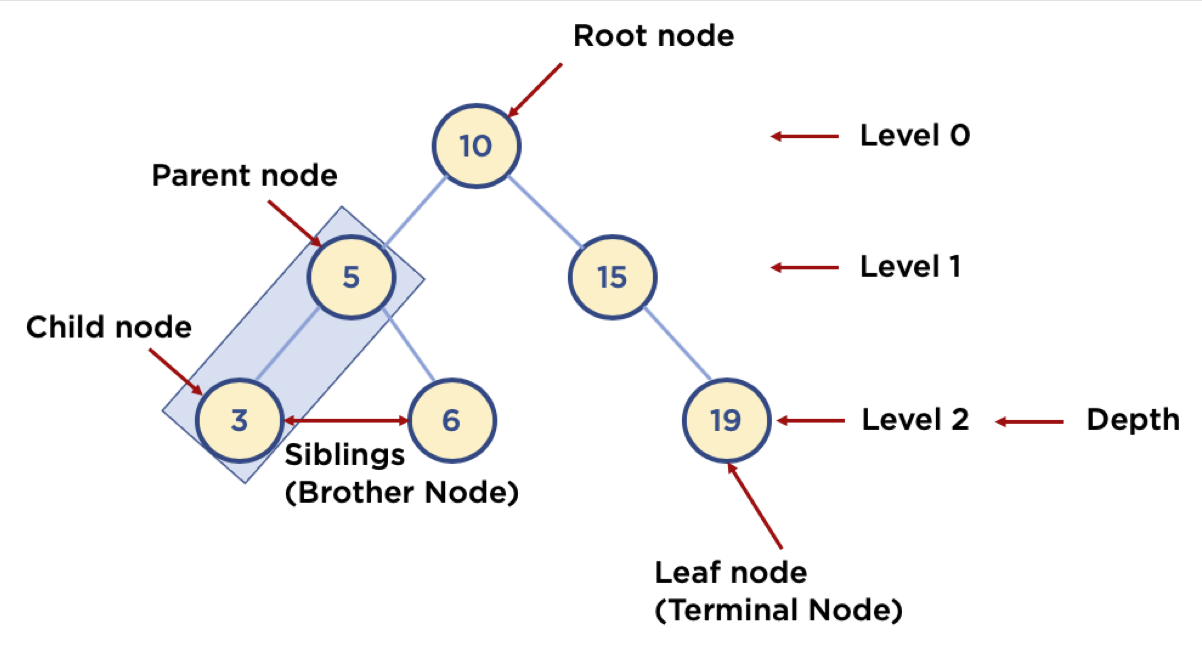 출처 : https://www.fun-coding.org/Chapter10-tree.html 트리 관련 용어 정리
출처 : https://www.fun-coding.org/Chapter10-tree.html 트리 관련 용어 정리 트리의 종류
- 이진 트리 (Binary Tree) : 노드의 최대 Branch가 2인 트리
- 완전 이진 트리 (Complete Binary Tree) : 노드를 삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리
- 전 이진 트리 (Full Binary Tree) : 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
- 포화 이진 트리 (Perfect Binary Tree) : 모든 내부 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는 트리
- 편향 트리 (Skewed Tree) : 한쪽으로 기울어진 트리, 사향 트리라고도 부름
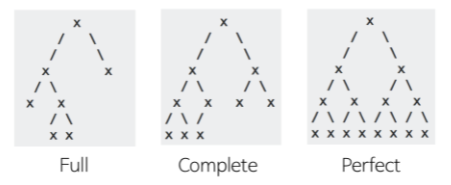 출처 : https://velog.io/@adam2/TREE 이진 트리의 종류
출처 : https://velog.io/@adam2/TREE 이진 트리의 종류
이진 탐색 트리 (Binary Search Tree, BST)
왼쪽 노드는 해당 노드보다 작거나 같은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지는 추가적인 조건이 있는 이진 트리
 출처 : https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node 이진 탐색 트리
출처 : https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node 이진 탐색 트리 Continue reading
Hash Table 해시 테이블
- 키(Key)에 데이터(Value)를 저장하는 데이터 구조
- Key를 통해 바로 데이터를 받아올 수 있으므로, 속도가 획기적으로 빨라짐
- 보통 배열로 미리 Hash Table 사이즈만큼 생성 후에 사용 (공간과 탐색 시간을 맞바꾸는 기법)
- 캐쉬를 구현하는 등의 검색, 저장, 삭제, 읽기가 많이 필요한 경우 사용
- 파이썬에서는 dictionary 타입으로 해시 테이블을 구현 가능
Continue reading
Singly Linked List 단일 연결 리스트
- 순차적으로 연결된 공간에 데이터를 나열하는 배열과 달리 링크드 리스트는 떨어진 곳에 존재하는 데이터를 연결해서 관리하는 데이터 구조
- 파이썬은 리스트 타입이 링크드 리스트의 기능을 모두 지원해 줌
- Node = data + link
노드(Node)
- 데이터 저장 단위 (데이터값, 포인터) 로 구성
포인터(pointer)
- 각 노드 안에서, 다음이나 이전의 노드와의 연결 정보를 가지고 있는 공간
Continue reading
제한된 접근(삽입, 삭제)만 허용 (Stack, Queue, Dequeue 모두 동일)
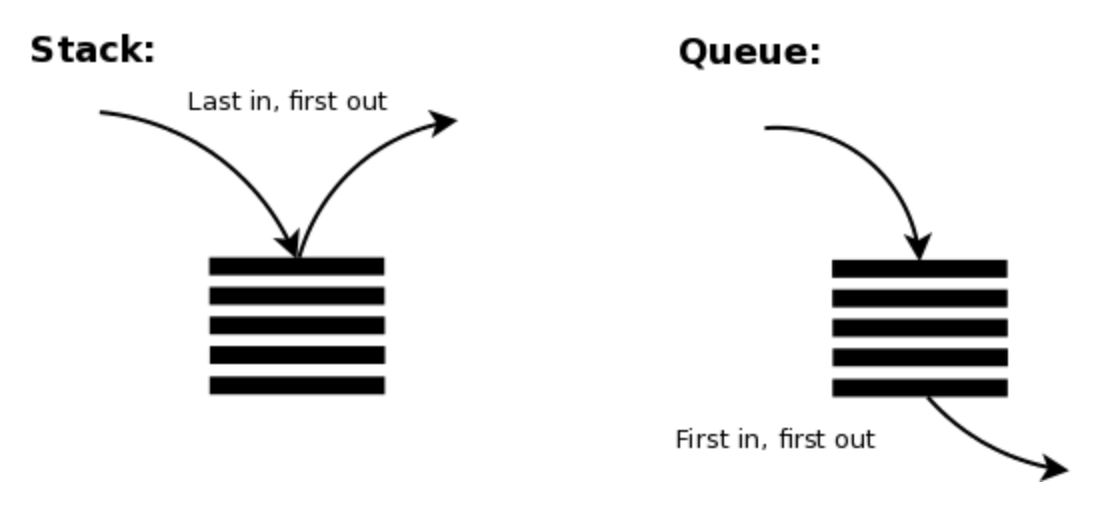 출처 : https://gohighbrow.com/stacks-and-queues/ 스택과 큐의 구조를 가장 잘 보여주는 예시
출처 : https://gohighbrow.com/stacks-and-queues/ 스택과 큐의 구조를 가장 잘 보여주는 예시
Stack 스택
```python class Stack: def init(self): self.items = []. #데이터 저장을 위한 리스트 준비
def push(self, val):
self.items.append(val)
Continue reading
Array 배열
특징
- 연속된 메모리 공간에 할당
- 무작위 접근(Random Access) 가능
- 정적 배열
- 지역성을 가짐
- 탐색에 효율적
장점
- 인덱스를 통한 검색에 빠른 성능을 보여줌
- 연속적 메모리 공간에 할당되어 순차 접근도 빠름
단점
- 한 데이터를 삭제 하더라도 처음 할당 된 사이즈만큼 데이터가 없더라도 메모리를 차지하고 있어서 메모리 재사용이 불가능
- 정적이므로 배열의 크기를 정해주어야 함
- 삽입 삭제 시 요소들을 이동해야 해서 비효율적
- 선언시 지정한 배열의 크기를 변동 불가
List 리스트
특징
Continue reading













